Méthode graphique.. 3

Méthode simplexe.. 6

Méthode de base artificielle... 8

Le principe de dualité.. 10

Liste de la littérature utilisée... 12

Introduction

Certaines propriétés des systèmes d'inégalités linéaires ont été considérées dès la première moitié du XIXe siècle en relation avec certains problèmes de mécanique analytique. L'étude systématique des systèmes d'inégalités linéaires a commencé à la toute fin du XIXe siècle, mais il n'est devenu possible de parler de théorie des inégalités linéaires qu'à la fin des années vingt du XXe siècle, lorsqu'un nombre suffisant de résultats les concernant ont eu déjà accumulé.

Or, la théorie des systèmes finis d'inégalités linéaires peut être considérée comme une branche de l'algèbre linéaire, qui en est issue avec l'exigence supplémentaire d'ordonner le champ des coefficients.

Les inégalités linéaires sont particulièrement importantes pour les économistes, car c'est à l'aide d'inégalités linéaires que l'on peut modéliser les processus de production et trouver les plans les plus rentables pour la production, le transport, l'allocation des ressources, etc.

Cet article présentera les méthodes de base pour résoudre les inégalités linéaires appliquées à des problèmes spécifiques.

Méthode graphique

La méthode graphique consiste à construire un ensemble de solutions admissibles au PLP, et à trouver dans cet ensemble le point correspondant à la fonction objectif max/min.

En raison des possibilités limitées de représentation graphique visuelle, cette méthode n'est utilisée que pour les systèmes d'inégalités linéaires à deux inconnues et les systèmes pouvant être réduits à cette forme.

Afin de démontrer clairement la méthode graphique, résolvons le problème suivant :

Dans un premier temps, il est nécessaire de construire une région de solutions réalisables. Pour cet exemple, il est plus pratique de sélectionner X2 comme abscisse et X1 comme ordonnée, et d'écrire les inégalités sous la forme suivante :

les graphiques et la zone de solutions réalisables se situent au premier trimestre.

Afin de trouver les points limites, nous résolvons les équations (1)=(2), (1)=(3) et (2)=(3).

Comme le montre l’illustration, le polyèdre ABCDE forme une région de solutions réalisables.

Si la région des solutions réalisables n'est pas fermée, alors soit max(f)=+ ∞ soit min(f)= -∞.

Nous pouvons maintenant procéder à la recherche directe du maximum de la fonction f.

En substituant alternativement les coordonnées des sommets du polyèdre dans la fonction f et en comparant les valeurs, on constate que

f(C)=f(4;1)=19 – maximum de la fonction.

Cette approche est très bénéfique avec un petit nombre de sommets. Mais cette procédure peut prendre beaucoup de temps s'il y a beaucoup de sommets.

Dans ce cas, il est plus pratique de considérer une ligne de niveau de la forme f=a. Avec une augmentation monotone du nombre a de -∞ à +∞, les droites f=a se déplacent le long du vecteur normal. Si, avec un tel mouvement de la ligne de niveau, il existe un certain point X - le premier point commun de la région des solutions réalisables (polyèdre ABCDE) et de la ligne de niveau, alors f(X) est le minimum de f sur l'ensemble ABCDE. Si X est le dernier point d'intersection de la ligne de niveau et de l'ensemble ABCDE, alors f(X) est le maximum sur l'ensemble des solutions réalisables. Si, comme a→-∞, la droite f=a coupe l'ensemble des solutions réalisables, alors min(f)= -∞. Si cela se produit sous la forme a→+∞, alors

Dans notre exemple, la droite f=a coupe la zone ABCDE au point C(4;1). Puisqu'il s'agit du dernier point d'intersection, max(f)=f(C)=f(4;1)=19.

Méthode simplexe

Les vrais problèmes de programmation linéaire contiennent un très grand nombre de contraintes et d’inconnues et sont exécutés sur un ordinateur. La méthode du simplexe est l’algorithme le plus général utilisé pour résoudre de tels problèmes. L'essence de la méthode est qu'après un certain nombre de transformations simplesx spéciales, le ZLP, réduit à une forme spéciale, est résolu. Afin de démontrer la méthode du simplexe en action, nous allons résoudre le problème suivant, accompagné de commentaires :

Afin de commencer à résoudre le problème par la méthode simplex, vous devez présenter le problème sous un formulaire spécial et remplir le tableau simplex.

Le système (4) constitue une limitation naturelle et ne rentre pas dans le tableau. Les équations (1), (2), (3) forment la région des solutions réalisables. L'expression (5) est la fonction objectif. Les termes libres dans le système de restrictions et la zone de solutions admissibles doivent être non négatifs.

Dans cet exemple, X3, X4, X5 sont les inconnues de base. Ils doivent être exprimés en termes d'inconnues libres et remplacés dans la fonction objectif.

Vous pouvez maintenant commencer à remplir le tableau simplex :

B.	X1	X2	X3	X4	X5	C
X3	0	-1	1	1	0	1
X4	0	1	-1	0	1	1
X5	1	1	1	0	0	2
F	0	-6	7	0	0	3

La première colonne de ce tableau indique les inconnues de base, la dernière - les valeurs des inconnues libres et le reste - les coefficients des inconnues.

Afin de trouver le maximum de la fonction f, à l'aide des transformations gaussiennes, vous devez vous assurer que tous les coefficients des inconnues de la dernière ligne sont non négatifs (pour trouver le minimum, assurez-vous que tous les coefficients sont inférieurs ou égaux à zéro).

B	X1	X2	X3	X4	X5	C
X3	-1	1	1	0	0	1
X4	1	-1	0	1	0	1
X5	1	1	0	0	1	2
F	-6	7	0	0	0	3

Pour cela, sélectionnez la colonne à coefficient négatif dans la dernière ligne (colonne 3) et composez la relation terme libre/coefficient (1/1 ; 2/1) pour les éléments positifs de cette colonne. Parmi ces ratios, sélectionnez le plus petit et marquez la ligne correspondante.

Nous avons sélectionné l'élément dans la cellule (3;3). Maintenant, en utilisant la méthode gaussienne, nous réinitialisons les autres coefficients de cette colonne, cela conduit à un changement de base et nous nous rapprochons de la solution optimale.

B	X1	X2	X3	X4	X5	C
X3	0	0	1	1	0	2
X1	1	-1	0	1	0	1
X5	0	2	0	-1	1	1
F	0	1	0	6	0	9

Comme le montre le tableau, tous les coefficients de la dernière ligne sont désormais supérieurs ou égaux à zéro. Cela signifie que nous avons trouvé la valeur optimale. Les inconnues libres sont égales à zéro, la valeur des inconnues de base et le maximum de la fonction f correspondent aux valeurs des inconnues libres.

Regardons des exemples sur la façon de résoudre un système d'inégalités linéaires.

4x + 29 \end(array) \right.\]" title="(!LANG : Rendu par QuickLaTeX.com">!}

Pour résoudre un système, vous avez besoin de chacune de ses inégalités constitutives. Seule la décision a été prise de ne pas écrire séparément, mais ensemble, en les combinant avec une accolade.

Dans chacune des inégalités du système, on déplace les inconnues d'un côté, les connues de l'autre de signe opposé :

Title="(!LANG : Rendu par QuickLaTeX.com">!}

Après simplification, les deux côtés de l’inégalité doivent être divisés par le nombre devant X. On divise la première inégalité par un nombre positif, donc le signe de l'inégalité ne change pas. On divise la deuxième inégalité par un nombre négatif, il faut donc inverser le signe de l'inégalité :

Title="(!LANG : Rendu par QuickLaTeX.com">!}

Nous marquons la solution des inégalités sur les droites numériques :

En réponse, nous notons l'intersection des solutions, c'est-à-dire la partie où les deux lignes sont ombrées.

Réponse : x∈[-2;1).

Dans la première inégalité, débarrassons-nous de la fraction. Pour ce faire, on multiplie les deux côtés terme par terme par le plus petit dénominateur commun 2. Lorsqu'il est multiplié par un nombre positif, le signe de l'inégalité ne change pas.

Dans la deuxième inégalité, nous ouvrons les parenthèses. Le produit de la somme et de la différence de deux expressions est égal à la différence des carrés de ces expressions. Sur le côté droit se trouve le carré de la différence entre les deux expressions.

Title="(!LANG : Rendu par QuickLaTeX.com">!}

On déplace les inconnues d'un côté, les connues de l'autre avec le signe opposé et on simplifie :

Nous divisons les deux côtés de l’inégalité par le nombre devant X. Dans la première inégalité, on divise par un nombre négatif, donc le signe de l’inégalité est inversé. Dans la seconde, on divise par un nombre positif, le signe de l'inégalité ne change pas :

Title="(!LANG : Rendu par QuickLaTeX.com">!}

Les deux inégalités ont un signe « inférieur à » (peu importe qu’un signe soit strictement « inférieur à », l’autre soit vague, « inférieur ou égal »). Nous ne pouvons pas marquer les deux solutions, mais utiliser la règle « ». Le plus petit est 1, donc le système se réduit à l'inégalité

Nous marquons sa solution sur la droite numérique :

Réponse : x∈(-∞;1].

Ouvrir les parenthèses. Dans la première inégalité - . Elle est égale à la somme des cubes de ces expressions.

Dans le second, le produit de la somme et de la différence de deux expressions, qui est égal à la différence des carrés. Comme ici il y a un signe moins devant les parenthèses, il est préférable de les ouvrir en deux étapes : utilisez d'abord la formule, puis ouvrez ensuite les parenthèses, en changeant le signe de chaque terme par le signe opposé.

On déplace les inconnues dans un sens, les connues dans l'autre avec le signe opposé :

Title="(!LANG : Rendu par QuickLaTeX.com">!}

Les deux sont supérieurs aux signes. En utilisant la règle du « plus que plus », nous réduisons le système d’inégalités à une seule inégalité. Le plus grand des deux nombres est 5, donc

Title="(!LANG : Rendu par QuickLaTeX.com">!}

Nous marquons la solution de l'inégalité sur la droite numérique et notons la réponse :

Réponse : x∈(5;∞).

Étant donné qu'en algèbre, les systèmes d'inégalités linéaires se rencontrent non seulement en tant que tâches indépendantes, mais également au cours de la résolution de divers types d'équations, d'inégalités, etc., il est important de maîtriser ce sujet en temps opportun.

La prochaine fois, nous examinerons des exemples de résolution de systèmes d'inéquations linéaires dans des cas particuliers où l'une des inégalités n'a pas de solution ou si sa solution est un nombre quelconque.

Catégorie : |

Une inégalité est constituée de deux nombres ou expressions mathématiques reliés par l'un des signes : > (supérieur à, dans le cas d'inégalités strictes),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

L'inégalité est linéaire dans les mêmes conditions que l'équation : elle ne contient des variables qu'au premier degré et ne contient pas de produits de variables.

La solution aux inégalités linéaires et aux systèmes d'inégalités linéaires est inextricablement liée à leur signification géométrique : la solution d'une inégalité linéaire est un certain demi-plan dans lequel le plan entier est divisé par une ligne droite, dont l'équation définit l'inégalité linéaire . Ce demi-plan, et dans le cas d'un système d'inégalités linéaires, la partie du plan limitée par plusieurs droites, doivent être retrouvés sur le dessin.

De nombreux problèmes économiques, en particulier les problèmes de programmation linéaire, dans lesquels il faut trouver le maximum ou le minimum d'une fonction, se réduisent à résoudre des systèmes d'inégalités linéaires avec un grand nombre de variables.

Résolution de systèmes d'inégalités linéaires avec un nombre quelconque d'inconnues

Examinons d’abord les inégalités linéaires dans le plan. Considérons une inégalité à deux variables et :

,

où sont les coefficients des variables (quelques nombres), est le terme libre (également un nombre).

Une inégalité à deux inconnues, comme une équation, a une infinité de solutions. La solution à cette inégalité est une paire de nombres qui satisfont cette inégalité. Géométriquement, l'ensemble des solutions à une inégalité est représenté comme un demi-plan délimité par une droite

,

que nous appellerons la ligne de démarcation.

Étape 1. Construire une ligne qui délimite l'ensemble des solutions à une inégalité linéaire

Pour ce faire, vous devez connaître deux points quelconques sur cette ligne. Trouvons les points d'intersection avec les axes de coordonnées. Ordonnée d'intersection UNégal à zéro (figure 1). Les valeurs numériques sur les axes de cette figure font référence à l'exemple 1, que nous analyserons immédiatement après cette excursion théorique.

On trouve l'abscisse en résolvant l'équation de la droite avec l'équation de l'axe en tant que système.

Trouvons l'intersection avec l'axe :

En substituant la valeur dans la première équation, nous obtenons

Où .

Ainsi, nous avons trouvé l'abscisse du point UN .

Trouvons les coordonnées du point d'intersection avec l'axe.

Points en abscisse Bégal à zéro. Résolvons l'équation de la ligne frontière avec l'équation de l'axe des coordonnées :

,

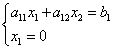
donc les coordonnées du point B: .

Étape 2. Tracez une ligne droite limitant l'ensemble des solutions à l'inégalité. Connaître les points UN Et B intersection de la ligne de démarcation avec les axes de coordonnées, nous pouvons tracer cette ligne. Une ligne droite (toujours figure 1) divise le plan entier en deux parties situées à droite et à gauche (au-dessus et en dessous) de cette ligne droite.

Étape 3. Déterminez quel demi-plan est la solution à cette inégalité. Pour ce faire, vous devez substituer l'origine des coordonnées (0 ; 0) dans cette inégalité. Si les coordonnées de l'origine satisfont à l'inégalité, alors la solution de l'inégalité est le demi-plan dans lequel se trouve l'origine des coordonnées. Si les coordonnées ne satisfont pas à l’inégalité, alors la solution de l’inégalité est un demi-plan qui ne contient pas l’origine. Le demi-plan de la solution de l'inégalité sera désigné par des traits allant de la ligne droite au demi-plan, comme sur la figure 1.

Si l'on résout un système d'inégalités linéaires, alors chaque étape est effectuée pour chacune des inégalités du système.

Exemple 1. Résoudre les inégalités

Solution. Traçons une ligne droite

En substituant une ligne droite dans l'équation, nous obtenons , et en substituant , nous obtenons . Par conséquent, les coordonnées des points d’intersection avec les axes seront UN(3; 0) , B(0 ; 2) . Traçons une ligne droite passant par ces points (encore une fois, figure 1).

Choisissons un demi-plan de solutions à l'inégalité. Pour ce faire, on substitue les coordonnées de l'origine (0 ; 0) dans l'inégalité :

on obtient , c'est-à-dire que les coordonnées de l'origine satisfont à cette inégalité. Par conséquent, la solution à l’inégalité est le demi-plan contenant l’origine des coordonnées, c’est-à-dire le demi-plan gauche (c’est-à-dire inférieur).

Si cette inégalité était stricte, elle aurait la forme

alors les points de la ligne frontière ne seraient pas une solution, puisqu’ils ne satisfont pas l’inégalité.

Considérons maintenant un système d'inégalités linéaires à deux inconnues :

Chacune des inégalités de ce système sur le plan définit un demi-plan. Un système d’inégalités linéaires est dit cohérent s’il a au moins une solution, et incohérent s’il n’a pas de solutions. Une solution d'un système d'inégalités linéaires est n'importe quelle paire de nombres () qui satisfait toutes les inégalités du système donné.

Géométriquement, la solution d'un système d'inégalités linéaires est l'ensemble des points qui satisfont toutes les inégalités du système, c'est-à-dire la partie commune des demi-plans résultants. Par conséquent, géométriquement, dans le cas général, la solution peut être représentée sous la forme d'un polygone ; dans un cas particulier, il peut s'agir d'une ligne, d'un segment ou même d'un point. Si un système d’inégalités linéaires est incohérent, alors il n’y a pas un seul point sur le plan qui satisfasse toutes les inégalités du système.

Exemple 2.

Solution. Il faut donc trouver un polygone de solutions à ce système d’inégalités. Construisons une ligne limite pour la première inégalité, c'est-à-dire une ligne, et une ligne limite pour la deuxième inégalité, c'est-à-dire une ligne.

Nous procédons cela étape par étape, comme cela a été montré dans la référence théorique et dans l'exemple 1, d'autant plus que dans l'exemple 1 nous avons construit une ligne frontière pour l'inégalité, qui est la première dans ce système.

Les demi-plans de solutions correspondant aux inégalités de ce système sont ombrés vers l'intérieur sur la figure 2. La partie commune des demi-plans de solution est un angle ouvert abc. Cela signifie que l'ensemble des points du plan qui constituent un angle ouvert abc, est une solution à la fois aux première et deuxième inégalités du système, c'est-à-dire qu'il s'agit d'une solution à un système de deux inégalités linéaires. En d’autres termes, les coordonnées de n’importe quel point de cet ensemble satisfont aux deux inégalités du système.

Exemple 3. Résoudre un système d'inégalités linéaires

Solution. Construisons des lignes frontières correspondant aux inégalités du système. Nous faisons cela en suivant les étapes données dans l’aide théorique pour chaque inégalité. Déterminons maintenant les demi-plans de solutions pour chaque inégalité (Figure 3).

Les demi-plans de solutions correspondant aux inégalités d'un système donné sont ombrés vers l'intérieur. L'intersection des demi-plans de solutions est représentée, comme le montre la figure, sous la forme d'un quadrilatère ABCE. Nous avons constaté que le polygone des solutions d'un système d'inégalités linéaires à deux variables est un quadrilatère ABCE .

Tout ce qui a été décrit ci-dessus sur les systèmes d'inégalités linéaires à deux inconnues s'applique également aux systèmes d'inégalités à n'importe quel nombre d'inconnues, à la seule différence que la solution de l'inégalité avec n les inconnues seront la totalité n nombres () satisfaisant toutes les inégalités, et au lieu de la ligne limite, il y aura un hyperplan frontière n-espace dimensionnel. La solution sera un polyèdre solution (simplex) délimité par des hyperplans.

ÉQUATIONS LINÉAIRES ET INÉGALITÉS I

§ 23 Systèmes d'inégalités linéaires

Un système d’inégalités linéaires est tout ensemble de deux ou plusieurs inégalités linéaires contenant la même quantité inconnue.

Des exemples de tels systèmes incluent les systèmes suivants :

Résoudre un système d'inégalités signifie trouver toutes les valeurs de la quantité inconnue pour lesquelles chaque inégalité du système est satisfaite.

Résolvons les systèmes ci-dessus.

Plaçons deux droites numériques l'une en dessous de l'autre (Fig. 31) ; en haut, nous marquons ces valeurs X , pour lequel la première inégalité est satisfaite ( X > 1), et en bas ces valeurs X , pour lequel la deuxième inégalité est satisfaite ( X > 4).

En comparant les résultats sur les droites numériques, nous remarquons que les deux inégalités seront simultanément satisfaites lorsque X > 4. Répondez, X > 4.

La première inégalité donne -3 X < -б, или X > 2, et le deuxième - X > -8, ou X < 8. Далее поступаем так же, как и в первом примере. На одной числовой прямой отмечаем все те значения X , pour lequel la première inégalité du système est satisfaite, et sur la deuxième droite numérique, située sous la première, toutes ces valeurs X , pour lequel la deuxième inégalité du système est satisfaite (Fig. 32).

Une comparaison de ces deux résultats montre que les deux inégalités seront valables simultanément pour toutes les valeurs X , compris entre 2 et 8. L'ensemble de ces valeurs X écrit comme double inégalité 2< X < 8.

Exemple 3. Résoudre le système d'inégalités

La première inégalité du système donne 5 X < 10, или X < 2, второе X > 4. Ainsi, tout nombre qui satisfait simultanément les deux inégalités ne doit pas être supérieur à 2 et supérieur à 4 (Fig. 33).

Mais de tels chiffres n’existent pas. Par conséquent, ce système d’inégalités ne s’applique à aucune valeur X . De tels systèmes d'inégalités sont appelés incohérents.

Des exercices

Résolvez ces systèmes d'inégalités (n° 179-184) :

Résoudre les inégalités (No. 185, 186) :

185. (2X + 3) (2 - 2X ) > 0. 186. (2 - π ) (2X - 15) (X + 4) > 0.

Recherchez les valeurs valides des lettres incluses dans les données d'égalité (n° 187, 188) :

Résoudre les inégalités (No. 189, 190) :

189. 1 < 2X - 5 < 2. 190. -2 < 1 - Oh < 5.

191. Quelle doit être la température de 10 litres d'eau pour les mélanger avec 6 litres d'eau à une température de 15° pour obtenir une eau à une température d'au moins 30° et pas plus de 40° ?

192. Un côté du triangle mesure 4 cm et la somme des deux autres est 10 cm. Trouvez ces côtés s'ils sont exprimés en nombres entiers.

193. On sait que le système de deux inégalités linéaires n'est satisfait pour aucune valeur de la quantité inconnue. Pouvons-nous dire que les inégalités individuelles de ce système ne sont satisfaites pour aucune valeur de la quantité inconnue ?

Matériaux additionnels
Chers utilisateurs, n'oubliez pas de laisser vos commentaires, avis, souhaits ! Tous les documents ont été vérifiés par un programme antivirus.

Supports pédagogiques et simulateurs dans la boutique en ligne Integral pour la 9e année
Manuel interactif pour la 9e année "Règles et exercices de géométrie"
Manuel électronique "Géométrie compréhensible" pour les classes 7-9

Système d'inégalités

Les gars, vous avez étudié les inégalités linéaires et quadratiques et appris à résoudre des problèmes sur ces sujets. Passons maintenant à un nouveau concept en mathématiques : le système d'inégalités. Un système d'inégalités est semblable à un système d'équations. Vous souvenez-vous des systèmes d’équations ? Vous avez étudié des systèmes d'équations en septième année, essayez de vous rappeler comment vous les avez résolus.

Introduisons la définition d'un système d'inégalités.
Plusieurs inégalités avec une variable x forment un système d'inégalités si vous avez besoin de trouver toutes les valeurs de x pour lesquelles chacune des inégalités forme une expression numérique correcte.

Toute valeur de x pour laquelle chaque inégalité prend l'expression numérique correcte est une solution à l'inégalité. Peut également être appelé une solution privée.
Qu'est-ce qu'une solution privée ? Par exemple, dans la réponse, nous avons reçu l'expression x>7. Alors x=8, ou x=123, ou tout autre nombre supérieur à sept est une solution particulière, et l'expression x>7 est une solution générale. La solution générale est formée de nombreuses solutions privées.

Comment avons-nous combiné le système d’équations ? C'est vrai, une accolade, et donc ils font la même chose avec les inégalités. Regardons un exemple de système d'inégalités : $\begin(cases)x+7>5\\x-3
Si le système d'inégalités est constitué d'expressions identiques, par exemple $\begin(cases)x+7>5\\x+7
Alors, qu’est-ce que cela signifie : trouver une solution à un système d’inégalités ?
Une solution à une inégalité est un ensemble de solutions partielles à une inégalité qui satisfont à la fois les deux inégalités du système.

Nous écrivons la forme générale du système d'inégalités sous la forme $\begin(cases)f(x)>0\\g(x)>0\end(cases)$

Notons $Х_1$ comme la solution générale de l'inégalité f(x)>0.
$X_2$ est la solution générale de l'inégalité g(x)>0.
$X_1$ et $X_2$ sont un ensemble de solutions particulières.
La solution au système d'inégalités sera des nombres appartenant à la fois à $X_1$ et à $X_2$.
Rappelons les opérations sur les décors. Comment trouver les éléments d’un ensemble qui appartiennent aux deux ensembles à la fois ? C'est vrai, il existe une opération d'intersection pour cela. Ainsi, la solution de notre inégalité sera l'ensemble $A= X_1∩ X_2$.

Exemples de solutions aux systèmes d’inégalités

Regardons des exemples de résolution de systèmes d'inégalités.

Résoudre le système d'inégalités.
a) $\begin(cases)3x-1>2\\5x-10 b) $\begin(cases)2x-4≤6\\-x-4
Solution.
a) Résolvez chaque inéquation séparément.
$3x-1>2 ; \; 3x>3 ; \; x>1$.
$5x-10
Marquons nos intervalles sur une ligne de coordonnées.

La solution du système sera le segment d'intersection de nos intervalles. L'inégalité est stricte, alors le segment sera ouvert.
Réponse : (1 ; 3).

B) Nous résoudrons également chaque inégalité séparément.
2x-4≤6 $ ; 2x≤ 10 ; x ≤ 5 $.
$-x-4 -5$.


La solution du système sera le segment d'intersection de nos intervalles. La deuxième inégalité est stricte, alors le segment sera ouvert à gauche.
Réponse : (-5 ; 5].

Résumons ce que nous avons appris.
Disons qu'il faut résoudre le système d'inégalités : $\begin(cases)f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end(cases)$.
Alors, l'intervalle ($x_1 ; x_2$) est la solution de la première inégalité.
L'intervalle ($y_1; y_2$) est la solution de la deuxième inégalité.
La solution d’un système d’inégalités est l’intersection des solutions de chaque inégalité.

Les systèmes d'inégalités peuvent comprendre non seulement des inégalités de premier ordre, mais également tout autre type d'inégalités.

Règles importantes pour résoudre les systèmes d'inégalités.
Si l’une des inégalités du système n’a pas de solution, alors le système tout entier n’a pas de solution.
Si l'une des inégalités est satisfaite pour n'importe quelle valeur de la variable, alors la solution du système sera la solution de l'autre inégalité.

Exemples.
Résoudre le système d'inégalités :$\begin(cases)x^2-16>0\\x^2-8x+12≤0 \end(cases)$
Solution.
Résolvons chaque inégalité séparément.
$x^2-16>0$.
$(x-4)(x+4)>0$.

Résolvons la deuxième inégalité.
$x^2-8x+12≤0$.
$(x-6)(x-2)≤0$.

La solution de l'inégalité est l'intervalle.
Traçons les deux intervalles sur la même ligne et trouvons l'intersection.
L'intersection des intervalles est le segment (4 ; 6).
Réponse : (4;6].

Résoudre le système d'inégalités.
a) $\begin(cases)3x+3>6\\2x^2+4x+4 b) $\begin(cases)3x+3>6\\2x^2+4x+4>0\end(cases )$.

Solution.
a) La première inégalité a une solution x>1.
Trouvons le discriminant de la deuxième inégalité.
$D=16-4 * 2 * 4=-16$. $D Rappelons la règle : lorsqu'une des inégalités n'a pas de solution, alors tout le système n'a pas de solution.
Réponse : Il n’y a pas de solutions.

B) La première inégalité a une solution x>1.
La deuxième inégalité est supérieure à zéro pour tout x. Alors la solution du système coïncide avec la solution de la première inégalité.
Réponse : x>1.

Problèmes sur les systèmes d'inégalités pour une solution indépendante

Résoudre des systèmes d’inégalités :
a) $\begin(cases)4x-5>11\\2x-12 b) $\begin(cases)-3x+1>5\\3x-11 c) $\begin(cases)x^2-25 d) $\begin(cases)x^2-16x+55>0\\x^2-17x+60≥0 \end(cases)$
e) $\begin(cas)x^2+36