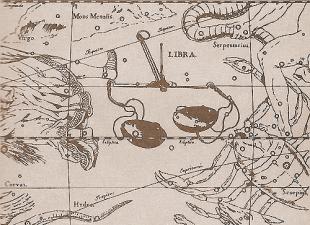
วิธีกราฟิก..3

วิธีเริม..6

วิธีการพื้นฐานประดิษฐ์...8

หลักความเป็นคู่..10

รายชื่อวรรณกรรมที่ใช้แล้ว...12

การแนะนำ

คุณสมบัติบางอย่างของระบบความไม่เท่าเทียมกันเชิงเส้นได้รับการพิจารณาย้อนกลับไปในช่วงครึ่งแรกของศตวรรษที่ 19 โดยเกี่ยวข้องกับปัญหาบางประการของกลศาสตร์การวิเคราะห์ การศึกษาระบบความไม่เท่าเทียมกันเชิงเส้นอย่างเป็นระบบเริ่มขึ้นเมื่อปลายศตวรรษที่ 19 แต่ก็มีความเป็นไปได้ที่จะพูดคุยเกี่ยวกับทฤษฎีความไม่เท่าเทียมกันเชิงเส้นเฉพาะในช่วงปลายศตวรรษที่ 20 เมื่อมีผลลัพธ์ที่เกี่ยวข้องกับระบบเหล่านี้เพียงพอ สะสมไว้แล้ว

ตอนนี้ทฤษฎีของระบบอัน จำกัด ของความไม่เท่าเทียมกันเชิงเส้นถือได้ว่าเป็นสาขาหนึ่งของพีชคณิตเชิงเส้นซึ่งขยายออกไปพร้อมกับข้อกำหนดเพิ่มเติมในการสั่งซื้อสนามสัมประสิทธิ์

ความไม่เท่าเทียมกันเชิงเส้นมีความสำคัญอย่างยิ่งสำหรับนักเศรษฐศาสตร์ เนื่องจากด้วยความช่วยเหลือของความไม่เท่าเทียมกันเชิงเส้น เราสามารถจำลองกระบวนการผลิตและค้นหาแผนการทำกำไรสูงสุดสำหรับการผลิต การขนส่ง การจัดสรรทรัพยากร ฯลฯ

บทความนี้จะสรุปวิธีการพื้นฐานในการแก้ไขอสมการเชิงเส้นที่ใช้กับปัญหาเฉพาะ

วิธีการแบบกราฟิก

วิธีการแบบกราฟิกประกอบด้วยการสร้างชุดวิธีแก้ปัญหาที่ยอมรับได้สำหรับ PLP และการค้นหาในจุดนี้จะสอดคล้องกับฟังก์ชันวัตถุประสงค์สูงสุด/นาที

เนื่องจากความเป็นไปได้ที่จำกัดในการแสดงภาพกราฟิก วิธีนี้จึงใช้เฉพาะกับระบบที่มีความไม่เท่ากันเชิงเส้นที่ไม่ทราบค่าสองตัว และระบบที่สามารถลดให้อยู่ในรูปแบบนี้ได้

เพื่อแสดงให้เห็นวิธีการแบบกราฟิกอย่างชัดเจน เรามาแก้ไขปัญหาต่อไปนี้:

ในขั้นแรก จำเป็นต้องสร้างขอบเขตของแนวทางแก้ไขที่เป็นไปได้ สำหรับตัวอย่างนี้จะสะดวกที่สุดในการเลือก X2 เป็น abscissa และ X1 เป็นลำดับ และเขียนอสมการในรูปแบบต่อไปนี้:

ทั้งกราฟและพื้นที่การแก้ปัญหาที่เป็นไปได้อยู่ในช่วงไตรมาสแรก

เพื่อที่จะหาจุดขอบเขต เราจะแก้สมการ (1)=(2), (1)=(3) และ (2)=(3)

ดังที่เห็นได้จากภาพประกอบ รูปทรงหลายเหลี่ยม ABCDE ก่อให้เกิดขอบเขตของคำตอบที่เป็นไปได้

ถ้าขอบเขตของการแก้ปัญหาที่เป็นไปได้ไม่ปิด ดังนั้น max(f)=+ ∞ หรือ min(f)= -∞

ตอนนี้เราสามารถดำเนินการค้นหาค่าสูงสุดของฟังก์ชัน f ได้โดยตรงแล้ว

โดยการสลับพิกัดของจุดยอดของรูปทรงหลายเหลี่ยมเป็นฟังก์ชัน f และเปรียบเทียบค่าต่างๆ เราพบว่า

f(C)=f(4;1)=19 – ค่าสูงสุดของฟังก์ชัน

แนวทางนี้ค่อนข้างมีประโยชน์เมื่อมีจุดยอดจำนวนน้อย แต่ขั้นตอนนี้อาจใช้เวลานานหากมีจุดยอดค่อนข้างมาก

ในกรณีนี้ จะสะดวกกว่าหากพิจารณาเส้นระดับในรูปแบบ f=a เมื่อเพิ่มจำนวน a จาก -∞ ถึง +∞ แบบโมโนโทนิก เส้นตรง f=a จะเลื่อนไปตามเวกเตอร์ปกติ หากด้วยการเคลื่อนที่ของเส้นระดับดังกล่าว มีจุด X จุดหนึ่ง - จุดร่วมจุดแรกของขอบเขตของคำตอบที่เป็นไปได้ (รูปทรงหลายเหลี่ยม ABCDE) และเส้นระดับ ดังนั้น f(X) คือค่าต่ำสุดของ f บนเซต เอบีดีอี. ถ้า X เป็นจุดตัดสุดท้ายของเส้นระดับกับเซต ABCDE แล้ว f(X) คือค่าสูงสุดบนเซตของคำตอบที่เป็นไปได้ หาก a→-∞ เส้นตรง f=a ตัดกับเซตของคำตอบที่เป็นไปได้ แล้ว min(f)= -∞ หากสิ่งนี้เกิดขึ้นเป็น→+∞แล้ว

ในตัวอย่างของเรา เส้นตรง f=a ตัดกันพื้นที่ ABCDE ที่จุด C(4;1) เนื่องจากนี่คือจุดตัดสุดท้าย สูงสุด(f)=f(C)=f(4;1)=19

วิธีเริม

ปัญหาการเขียนโปรแกรมเชิงเส้นจริงมีข้อจำกัดและสิ่งไม่รู้จำนวนมาก และดำเนินการบนคอมพิวเตอร์ วิธีซิมเพล็กซ์เป็นอัลกอริธึมทั่วไปที่ใช้แก้ปัญหาดังกล่าว สาระสำคัญของวิธีนี้คือหลังจากการแปลงซิมเพล็กซ์พิเศษจำนวนหนึ่ง ZLP ซึ่งลดลงเป็นรูปแบบพิเศษก็ได้รับการแก้ไข เพื่อสาธิตวิธีปฏิบัติแบบซิมเพล็กซ์ ให้เราแก้ไขปัญหาต่อไปนี้พร้อมข้อคิดเห็นประกอบ:

ในการเริ่มแก้ไขปัญหาด้วยวิธีซิมเพล็กซ์ คุณต้องนำปัญหามาไว้ในแบบฟอร์มพิเศษและกรอกตารางซิมเพล็กซ์

ระบบ (4) เป็นข้อจำกัดตามธรรมชาติและไม่เหมาะกับตาราง สมการ (1), (2), (3) ก่อให้เกิดขอบเขตของคำตอบที่เป็นไปได้ นิพจน์ (5) คือฟังก์ชันวัตถุประสงค์ ข้อกำหนดฟรีในระบบข้อจำกัดและขอบเขตของโซลูชันที่ยอมรับได้จะต้องไม่เป็นค่าลบ

ในตัวอย่างนี้ X3, X4, X5 เป็นสิ่งที่ไม่ทราบพื้นฐาน จะต้องแสดงออกมาในรูปของสิ่งไม่รู้อิสระและแทนที่ในฟังก์ชันวัตถุประสงค์

ตอนนี้คุณสามารถเริ่มกรอกตารางซิมเพล็กซ์ได้แล้ว:

บี.	X1	X2	X3	X4	X5	ค
X3	0	-1	1	1	0	1
X4	0	1	-1	0	1	1
X5	1	1	1	0	0	2
ฉ	0	-6	7	0	0	3

คอลัมน์แรกของตารางนี้ระบุค่าไม่ทราบพื้นฐาน ค่าสุดท้าย - ค่าของค่าไม่ทราบอิสระ และส่วนที่เหลือ - ค่าสัมประสิทธิ์ของค่าไม่ทราบ

เพื่อที่จะหาค่าสูงสุดของฟังก์ชัน f โดยใช้การแปลงแบบเกาส์เซียน คุณต้องแน่ใจว่าสัมประสิทธิ์ทั้งหมดของค่าที่ไม่รู้จักในแถวสุดท้ายไม่เป็นค่าลบ (หากต้องการหาค่าต่ำสุด ตรวจสอบให้แน่ใจว่าค่าสัมประสิทธิ์ทั้งหมดน้อยกว่าหรือเท่ากัน ให้เป็นศูนย์)

บี	X1	X2	X3	X4	X5	ค
X3	-1	1	1	0	0	1
X4	1	-1	0	1	0	1
X5	1	1	0	0	1	2
ฉ	-6	7	0	0	0	3

เมื่อต้องการทำเช่นนี้ ให้เลือกคอลัมน์ที่มีค่าสัมประสิทธิ์ลบในแถวสุดท้าย (คอลัมน์ 3) และเขียนความสัมพันธ์ระยะ/สัมประสิทธิ์อิสระ (1/1; 2/1) สำหรับองค์ประกอบเชิงบวกของคอลัมน์นี้ จากอัตราส่วนเหล่านี้ ให้เลือกอัตราส่วนที่เล็กที่สุดและทำเครื่องหมายบรรทัดที่เกี่ยวข้อง

เราได้เลือกองค์ประกอบในเซลล์ (3;3) ตอนนี้ เมื่อใช้วิธีเกาส์เซียน เราจะรีเซ็ตค่าสัมประสิทธิ์อื่นๆ ในคอลัมน์นี้ ซึ่งนำไปสู่การเปลี่ยนแปลงในพื้นฐาน และเราเข้าใกล้วิธีแก้ปัญหาที่ดีที่สุดไปอีกขั้นแล้ว

บี	X1	X2	X3	X4	X5	ค
X3	0	0	1	1	0	2
X1	1	-1	0	1	0	1
X5	0	2	0	-1	1	1
ฉ	0	1	0	6	0	9

ดังที่เห็นจากตาราง ตอนนี้ค่าสัมประสิทธิ์ทั้งหมดในแถวสุดท้ายมากกว่าหรือเท่ากับศูนย์ ซึ่งหมายความว่าเราพบค่าที่เหมาะสมที่สุดแล้ว ค่าที่ไม่รู้จักฟรีมีค่าเท่ากับศูนย์ ค่าของค่าที่ไม่รู้จักพื้นฐาน และค่าสูงสุดของฟังก์ชัน f สอดคล้องกับค่าของค่าที่ไม่ทราบค่าฟรี

ลองดูตัวอย่างวิธีแก้ปัญหาระบบอสมการเชิงเส้น

4x + 29 \end(array) \right.\]" title="แสดงผลโดย QuickLaTeX.com">!}

ในการแก้ปัญหาระบบ คุณต้องมีองค์ประกอบที่ไม่เท่าเทียมกันแต่ละอย่าง มีเพียงการตัดสินใจเท่านั้นที่จะไม่เขียนแยกกัน แต่รวมเข้าด้วยกันด้วยเครื่องหมายปีกกา

ในแต่ละความไม่เท่าเทียมกันของระบบ เราย้ายสิ่งที่ไม่รู้จักไปด้านหนึ่ง และสิ่งที่รู้แล้วไปอีกด้านหนึ่งที่มีเครื่องหมายตรงกันข้าม:

Title="แสดงผลโดย QuickLaTeX.com">!}

หลังจากลดรูปลงแล้ว อสมการทั้งสองข้างจะต้องหารด้วยตัวเลขที่อยู่หน้า X เราหารอสมการแรกด้วยจำนวนบวก ดังนั้นเครื่องหมายของอสมการจึงไม่เปลี่ยนแปลง เราหารอสมการที่สองด้วยจำนวนลบ ดังนั้นเครื่องหมายอสมการจะต้องกลับด้าน:

Title="แสดงผลโดย QuickLaTeX.com">!}

เราทำเครื่องหมายวิธีแก้ปัญหาอสมการบนเส้นจำนวน:

ในการตอบสนอง เราเขียนจุดตัดของคำตอบ นั่นคือส่วนที่มีการแรเงาบนเส้นทั้งสอง

คำตอบ: x∈[-2;1)

ในอสมการแรก ลองกำจัดเศษส่วนออกไป. ในการทำเช่นนี้ เราจะคูณทั้งสองข้างด้วยตัวส่วนร่วมที่น้อยที่สุด 2 เมื่อคูณด้วยจำนวนบวก เครื่องหมายอสมการจะไม่เปลี่ยนแปลง

ในอสมการที่สองเราจะเปิดวงเล็บ ผลคูณของผลรวมและผลต่างของสองนิพจน์จะเท่ากับผลต่างของกำลังสองของนิพจน์เหล่านี้ ทางด้านขวาคือกำลังสองของความแตกต่างระหว่างสองนิพจน์

Title="แสดงผลโดย QuickLaTeX.com">!}

เราย้ายสิ่งที่ไม่รู้จักไปด้านหนึ่ง สิ่งที่รู้จักไปอีกด้านหนึ่งโดยมีเครื่องหมายตรงกันข้าม และทำให้ง่ายขึ้น:

เราหารทั้งสองด้านของอสมการด้วยตัวเลขหน้า X ในอสมการแรก เราหารด้วยจำนวนลบ ดังนั้นเครื่องหมายของอสมการจึงกลับกัน ประการที่สองหารด้วยจำนวนบวก เครื่องหมายอสมการไม่เปลี่ยนแปลง:

Title="แสดงผลโดย QuickLaTeX.com">!}

อสมการทั้งสองมีเครื่องหมาย "น้อยกว่า" (ไม่สำคัญว่าเครื่องหมายหนึ่งจะ "น้อยกว่า" อย่างเคร่งครัด ส่วนอีกเครื่องหมายหลวม "น้อยกว่าหรือเท่ากับ") เราไม่สามารถทำเครื่องหมายทั้งสองวิธีได้ แต่ใช้กฎ " " อันที่เล็กกว่าคือ 1 ดังนั้นระบบจึงลดความไม่เท่าเทียมกัน

เราทำเครื่องหมายวิธีแก้ปัญหาไว้บนเส้นจำนวน:

คำตอบ: x∈(-∞;1]

การเปิดวงเล็บ ในความไม่เท่าเทียมกันครั้งแรก - . มันเท่ากับผลรวมของกำลังสามของนิพจน์เหล่านี้

ประการที่สอง ผลคูณของผลรวมและผลต่างของสองนิพจน์ ซึ่งเท่ากับผลต่างของกำลังสอง เนื่องจากที่นี่มีเครื่องหมายลบอยู่หน้าวงเล็บ จึงเป็นการดีกว่าถ้าเปิดเป็นสองขั้นตอน: ขั้นแรกให้ใช้สูตร จากนั้นจึงเปิดวงเล็บโดยเปลี่ยนเครื่องหมายของแต่ละเทอมให้ตรงกันข้าม

เราย้ายสิ่งไม่รู้ไปในทิศทางเดียว สิ่งรู้ไปในทิศทางตรงกันข้ามด้วยเครื่องหมายตรงกันข้าม:

Title="แสดงผลโดย QuickLaTeX.com">!}

ทั้งสองยิ่งใหญ่กว่าสัญญาณ การใช้กฎ "มากกว่ามากกว่า" เราจะลดระบบความไม่เท่าเทียมกันให้เหลือเพียงความไม่เท่าเทียมกันเดียว จำนวนที่มากกว่าของทั้งสองจำนวนคือ 5 ดังนั้น

Title="แสดงผลโดย QuickLaTeX.com">!}

เราทำเครื่องหมายวิธีแก้ไขอสมการบนเส้นจำนวนแล้วเขียนคำตอบ:

คำตอบ: x∈(5;∞)

เนื่องจากในระบบพีชคณิตของอสมการเชิงเส้นเกิดขึ้นไม่เพียง แต่เป็นงานอิสระเท่านั้น แต่ยังอยู่ในหลักสูตรของการแก้สมการอสมการประเภทต่าง ๆ ฯลฯ สิ่งสำคัญคือต้องเชี่ยวชาญหัวข้อนี้ในเวลาที่เหมาะสม

คราวหน้าเราจะดูตัวอย่างการแก้ระบบอสมการเชิงเส้นในกรณีพิเศษ เมื่ออสมการตัวใดตัวหนึ่งไม่มีคำตอบหรือคำตอบเป็นตัวเลขใดๆ

หมวดหมู่: |

อสมการคือตัวเลขสองตัวหรือนิพจน์ทางคณิตศาสตร์ที่เชื่อมต่อกันด้วยเครื่องหมายตัวใดตัวหนึ่ง: > (มากกว่า ในกรณีของความไม่เท่าเทียมกันแบบเคร่งครัด)< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

ความไม่เท่าเทียมกันคือ เชิงเส้นภายใต้เงื่อนไขเดียวกันกับสมการ: ประกอบด้วยตัวแปรเพียงระดับแรกและไม่มีผลคูณของตัวแปร

การแก้อสมการเชิงเส้นและระบบอสมการเชิงเส้นนั้นเชื่อมโยงกับความหมายทางเรขาคณิตอย่างแยกไม่ออก การแก้อสมการเชิงเส้นคือระนาบครึ่งระนาบซึ่งระนาบทั้งหมดถูกหารด้วยเส้นตรง ซึ่งเป็นสมการที่กำหนดความไม่เท่าเทียมกันเชิงเส้น . ระนาบครึ่งระนาบนี้ และในกรณีของระบบความไม่เท่าเทียมกันเชิงเส้น จะต้องพบส่วนของระนาบที่ถูกจำกัดด้วยเส้นตรงหลายเส้นในภาพวาด

ปัญหาทางเศรษฐกิจจำนวนมาก โดยเฉพาะอย่างยิ่งปัญหาการโปรแกรมเชิงเส้นซึ่งจำเป็นต้องค้นหาค่าสูงสุดหรือต่ำสุดของฟังก์ชัน จะลดลงเหลือแค่การแก้ปัญหาระบบอสมการเชิงเส้นที่มีตัวแปรจำนวนมาก

การแก้ระบบอสมการเชิงเส้นด้วยค่าไม่ทราบจำนวนเท่าใดก็ได้

ก่อนอื่น ลองดูความไม่เท่าเทียมกันเชิงเส้นในระนาบ พิจารณาอสมการหนึ่งที่มีตัวแปรสองตัวและ:

,

โดยที่ค่าสัมประสิทธิ์ของตัวแปร (ตัวเลขบางตัว) คือเทอมอิสระ (ตัวเลขบางตัวด้วย)

อสมการหนึ่งกับสิ่งไม่รู้สองตัว เช่น สมการ มีวิธีแก้จำนวนอนันต์ วิธีแก้อสมการนี้คือคู่ตัวเลขที่ตรงกับอสมการนี้ ในเชิงเรขาคณิต ชุดของการแก้อสมการจะแสดงเป็นรูปครึ่งระนาบที่ล้อมรอบด้วยเส้นตรง

,

ซึ่งเราจะเรียกว่าเส้นเขตแดน

ขั้นตอนที่ 1 สร้างเส้นที่เชื่อมชุดของคำตอบเข้ากับอสมการเชิงเส้น

ในการทำเช่นนี้ คุณจำเป็นต้องรู้จุดสองจุดบนเส้นนี้ ลองหาจุดตัดกับแกนพิกัดกัน แยกบรรพชา กเท่ากับศูนย์ (รูปที่ 1) ค่าตัวเลขบนแกนในรูปนี้อ้างอิงถึงตัวอย่างที่ 1 ซึ่งเราจะวิเคราะห์ทันทีหลังจากการทัศนศึกษาเชิงทฤษฎีนี้

เราค้นหา Abscissa โดยการแก้สมการของเส้นตรงโดยใช้สมการของแกนเป็นระบบ

ลองหาจุดตัดกับแกน:

เราแทนค่าลงในสมการแรกแล้ว

ที่ไหน .

ดังนั้นเราจึงพบจุดอับซิสซาของจุดนั้น ก .

ลองหาพิกัดของจุดตัดกับแกนกัน

จุด Abscissa บีเท่ากับศูนย์ ลองแก้สมการของเส้นเขตแดนด้วยสมการของแกนพิกัด:

,

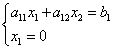
ดังนั้นพิกัดของจุดนั้น บี: .

ขั้นตอนที่ 2 วาดเส้นตรงเพื่อจำกัดชุดการแก้ปัญหาของอสมการรู้ประเด็นต่างๆ กและ บีจุดตัดของเส้นเขตแดนกับแกนพิกัด เราก็วาดเส้นนี้ได้ เส้นตรง (รูปที่ 1 อีกครั้ง) แบ่งระนาบทั้งหมดออกเป็นสองส่วนที่อยู่ทางขวาและซ้าย (ด้านบนและด้านล่าง) ของเส้นตรงนี้

ขั้นตอนที่ 3 พิจารณาว่าฮาล์ฟเพลนใดคือคำตอบของอสมการนี้ในการทำเช่นนี้ คุณต้องแทนที่จุดกำเนิดของพิกัด (0; 0) ลงในอสมการนี้ หากพิกัดของจุดกำเนิดเป็นไปตามความไม่เท่าเทียมกัน วิธีแก้ของอสมการก็คือแบบครึ่งระนาบซึ่งมีจุดกำเนิดของพิกัดอยู่ ถ้าพิกัดไม่เป็นไปตามอสมการ การแก้อสมการจะเป็นแบบครึ่งระนาบที่ไม่มีจุดกำเนิด ครึ่งระนาบของการแก้ปัญหาความไม่เท่าเทียมกันจะแสดงด้วยจังหวะจากเส้นตรงไปยังครึ่งระนาบ ดังในรูปที่ 1

ถ้าเราแก้ระบบอสมการเชิงเส้นจากนั้นแต่ละขั้นตอนจะดำเนินการสำหรับความไม่เท่าเทียมกันของระบบแต่ละอย่าง

ตัวอย่างที่ 1แก้ปัญหาความไม่เท่าเทียมกัน

สารละลาย. ลองวาดเส้นตรงกัน

เมื่อแทนเส้นตรงลงในสมการ เราจะได้ และแทนที่ เราจะได้ ดังนั้นพิกัดของจุดตัดกับแกนจะเป็นดังนี้ ก(3; 0) , บี(0; 2) . ลองวาดเส้นตรงผ่านจุดเหล่านี้กัน (รูปที่ 1 อีกครั้ง)

ให้เราเลือกคำตอบแบบครึ่งระนาบของอสมการ ในการดำเนินการนี้ เราจะแทนที่พิกัดของจุดกำเนิด (0; 0) ลงในความไม่เท่าเทียมกัน:

เราได้รับ เช่น พิกัดของแหล่งกำเนิดตอบสนองความไม่เท่าเทียมกันนี้ ดังนั้น วิธีแก้ปัญหาความไม่เท่าเทียมกันคือระนาบครึ่งระนาบที่มีจุดกำเนิดของพิกัด กล่าวคือ ระนาบครึ่งด้านซ้าย (หรือต่ำกว่า)

หากความไม่เท่าเทียมกันนี้เข้มงวดนั่นคือมันจะมีรูปแบบ

แล้วจุดของเส้นเขตแดนก็ไม่ใช่วิธีแก้ปัญหา เนื่องจากไม่เป็นไปตามความไม่เท่าเทียมกัน

ตอนนี้ให้พิจารณาระบบความไม่เท่าเทียมกันเชิงเส้นโดยมีสองสิ่งที่ไม่ทราบ:

อสมการแต่ละอย่างของระบบนี้บนระนาบจะกำหนดระนาบครึ่งระนาบ ระบบความไม่เท่าเทียมกันเชิงเส้นเรียกว่าสอดคล้องกันหากมีวิธีแก้ปัญหาอย่างน้อยหนึ่งข้อ และไม่สอดคล้องกันหากไม่มีวิธีแก้ปัญหา วิธีแก้ระบบอสมการเชิงเส้นคือคู่ของตัวเลขใดๆ () ที่เป็นค่าอสมการของระบบที่กำหนดทั้งหมด

ในเชิงเรขาคณิต คำตอบของระบบอสมการเชิงเส้นคือเซตของจุดที่เป็นไปตามอสมการทั้งหมดของระบบ ซึ่งก็คือส่วนร่วมของผลลัพธ์แบบครึ่งระนาบ ดังนั้น ในกรณีทั่วไปทางเรขาคณิต วิธีแก้ปัญหาสามารถแสดงเป็นรูปหลายเหลี่ยมบางรูปได้ ในบางกรณี อาจเป็นเส้นตรง ส่วน หรือแม้แต่จุดก็ได้ หากระบบความไม่เท่าเทียมกันเชิงเส้นไม่สอดคล้องกัน ก็ไม่มีจุดใดจุดหนึ่งบนระนาบที่ตอบสนองความไม่เท่าเทียมกันของระบบทั้งหมด

ตัวอย่างที่ 2

สารละลาย. ดังนั้นเราจึงต้องหารูปหลายเหลี่ยมของคำตอบของระบบอสมการนี้ ลองสร้างเส้นแบ่งเขตของอสมการอันแรก นั่นคือเส้นตรง และเส้นแบ่งเขตของอสมการอันที่สอง นั่นคือเส้นตรง

เราทำทีละขั้นตอน ดังที่แสดงในการอ้างอิงทางทฤษฎีและในตัวอย่างที่ 1 โดยเฉพาะอย่างยิ่งเนื่องจากในตัวอย่างที่ 1 เราได้สร้างเส้นแบ่งเขตสำหรับความไม่เท่าเทียมกัน ซึ่งเป็นเส้นแรกในระบบนี้

วิธีแก้ปัญหาแบบครึ่งระนาบที่สอดคล้องกับความไม่เท่าเทียมกันของระบบนี้จะถูกแรเงาไว้ด้านในในรูปที่ 2 ส่วนทั่วไปของระนาบครึ่งระนาบของสารละลายคือมุมเปิด เอบีซี- ซึ่งหมายความว่าเซตของจุดในระนาบที่ประกอบเป็นมุมเปิด เอบีซีเป็นวิธีแก้อสมการทั้งระบบที่หนึ่งและที่สอง กล่าวคือ เป็นคำตอบของระบบที่มีความไม่เท่าเทียมกันเชิงเส้นสองตัว กล่าวอีกนัยหนึ่ง พิกัดของจุดใดๆ จากชุดนี้เป็นไปตามความไม่เท่าเทียมกันของระบบ

ตัวอย่างที่ 3แก้ระบบอสมการเชิงเส้น

สารละลาย. ให้เราสร้างเส้นขอบเขตที่สอดคล้องกับความไม่เท่าเทียมกันของระบบ เราทำเช่นนี้โดยทำตามขั้นตอนที่ให้ไว้ในวิธีใช้ทางทฤษฎีสำหรับความไม่เท่าเทียมกันแต่ละรายการ ตอนนี้เรากำหนดครึ่งระนาบของคำตอบสำหรับความไม่เท่าเทียมกันแต่ละรายการ (รูปที่ 3)

วิธีแก้ปัญหาแบบครึ่งระนาบที่สอดคล้องกับความไม่เท่าเทียมกันของระบบที่กำหนดจะถูกแรเงาไว้ด้านใน จุดตัดของครึ่งระนาบของการแก้ปัญหาดังแสดงในรูปในรูปของรูปสี่เหลี่ยมขนมเปียกปูน เอบีซี- เราพบว่ารูปหลายเหลี่ยมของคำตอบของระบบความไม่เท่าเทียมกันเชิงเส้นที่มีตัวแปรสองตัวคือรูปสี่เหลี่ยมขนมเปียกปูน เอบีซี .

ทุกสิ่งที่อธิบายไว้ข้างต้นเกี่ยวกับระบบอสมการเชิงเส้นที่ไม่ทราบค่าสองตัวยังนำไปใช้กับระบบอสมการที่ไม่ทราบจำนวนเท่าใดก็ได้ โดยมีความแตกต่างเพียงอย่างเดียวคือการแก้ปัญหาอสมการด้วย nสิ่งไม่รู้จะเป็นจำนวนทั้งสิ้น nตัวเลข () เป็นไปตามความไม่เท่าเทียมกันทั้งหมดและแทนที่จะเป็นเส้นเขตแดนจะมีไฮเปอร์เพลนเขตแดน n-พื้นที่มิติ คำตอบจะเป็นวิธีแก้ปัญหารูปทรงหลายเหลี่ยม (ซิมเพล็กซ์) ที่ล้อมรอบด้วยไฮเปอร์เพลน

สมการเชิงเส้นและอสมการ I

§ 23 ระบบความไม่เท่าเทียมกันเชิงเส้น

ระบบความไม่เท่าเทียมกันเชิงเส้นคือชุดใดๆ ของความไม่เท่าเทียมกันเชิงเส้นตั้งแต่สองตัวขึ้นไปซึ่งมีปริมาณที่ไม่ทราบค่าเท่ากัน

ตัวอย่างของระบบดังกล่าวได้แก่ระบบต่อไปนี้:

การแก้ระบบอสมการหมายถึงการค้นหาค่าทั้งหมดของปริมาณที่ไม่รู้จักซึ่งเป็นไปตามความไม่เท่าเทียมกันของระบบ

มาแก้ระบบข้างต้นกัน

วางบรรทัดจำนวนสองบรรทัดไว้ใต้บรรทัดอื่น (รูปที่ 31) ด้านบนเราทำเครื่องหมายค่าเหล่านั้น เอ็กซ์ ซึ่งเป็นไปตามความไม่เท่าเทียมกันประการแรก ( เอ็กซ์ > 1) และที่ด้านล่างสุดของค่าเหล่านั้น เอ็กซ์ ซึ่งเป็นไปตามอสมการที่สอง ( เอ็กซ์ > 4).

เมื่อเปรียบเทียบผลลัพธ์บนเส้นจำนวน เราจะสังเกตเห็นว่าความไม่เท่าเทียมกันทั้งสองจะเกิดขึ้นพร้อมกันเมื่อใด เอ็กซ์ > 4. คำตอบ เอ็กซ์ > 4.

อสมการแรกให้ -3 เอ็กซ์ < -б, или เอ็กซ์ > 2 และอันที่สอง - เอ็กซ์ > -8 หรือ เอ็กซ์ < 8. Далее поступаем так же, как и в первом примере. На одной числовой прямой отмечаем все те значения เอ็กซ์ ซึ่งตรงกับความไม่เท่าเทียมกันแรกของระบบ และบนเส้นจำนวนที่สองซึ่งอยู่ใต้ค่าแรก ค่าเหล่านั้นทั้งหมด เอ็กซ์ ซึ่งเป็นไปตามความไม่เท่าเทียมกันที่สองของระบบ (รูปที่ 32)

การเปรียบเทียบผลลัพธ์ทั้งสองนี้แสดงให้เห็นว่าความไม่เท่าเทียมกันทั้งสองจะคงไว้สำหรับค่าทั้งหมดพร้อมกัน เอ็กซ์ ล้อมรอบตั้งแต่ 2 ถึง 8 ชุดของค่าดังกล่าว เอ็กซ์ เขียนเป็นอสมการสองเท่า 2< เอ็กซ์ < 8.

ตัวอย่างที่ 3 แก้ระบบความไม่เท่าเทียมกัน

อสมการแรกของระบบให้ 5 เอ็กซ์ < 10, или เอ็กซ์ < 2, второе เอ็กซ์ > 4. ดังนั้น จำนวนใดๆ ที่เป็นไปตามอสมการทั้งสองพร้อมกันจะต้องไม่เกิน 2 และมากกว่า 4 (รูปที่ 33)

แต่ไม่มีตัวเลขดังกล่าว ดังนั้นระบบอสมการนี้ไม่ถือเป็นค่าใดๆ เอ็กซ์ - ระบบความไม่เท่าเทียมกันดังกล่าวเรียกว่าไม่สอดคล้องกัน

การออกกำลังกาย

แก้ระบบความไม่เท่าเทียมกันเหล่านี้ (หมายเลข 179 -184):

แก้ความไม่เท่าเทียมกัน (ฉบับที่ 185, 186):

185. (2เอ็กซ์ + 3) (2 - 2เอ็กซ์ ) > 0. 186. (2 - π ) (2เอ็กซ์ - 15) (เอ็กซ์ + 4) > 0.

ค้นหาค่าที่ถูกต้องของตัวอักษรที่รวมอยู่ในข้อมูลความเท่าเทียมกัน (หมายเลข 187, 188):

แก้ความไม่เท่าเทียมกัน (ฉบับที่ 189, 190):

189. 1 < 2เอ็กซ์ - 5 < 2. 190. -2 < 1 - โอ้ < 5.

191. อุณหภูมิน้ำ 10 ลิตรควรเป็นเท่าใดจึงจะผสมกับน้ำ 6 ลิตรที่อุณหภูมิ 15° เพื่อให้ได้น้ำที่มีอุณหภูมิอย่างน้อย 30° และไม่เกิน 40°

192 ด้านหนึ่งของรูปสามเหลี่ยมคือ 4 ซม. และอีกสองด้านมีผลรวมเป็น 10 ซม. จงหาด้านเหล่านี้หากแสดงเป็นจำนวนเต็ม

193. เป็นที่ทราบกันดีว่าระบบของอสมการเชิงเส้นสองตัวไม่พอใจกับค่าใด ๆ ของปริมาณที่ไม่รู้จัก เราสามารถพูดได้ว่าความไม่เท่าเทียมกันส่วนบุคคลของระบบนี้ไม่พอใจกับค่าใด ๆ ของปริมาณที่ไม่รู้จักหรือไม่?

วัสดุเพิ่มเติม
เรียนผู้ใช้ อย่าลืมแสดงความคิดเห็น บทวิจารณ์ และความปรารถนาของคุณ! วัสดุทั้งหมดได้รับการตรวจสอบโดยโปรแกรมป้องกันไวรัส

เครื่องช่วยการศึกษาและเครื่องจำลองในร้านค้าออนไลน์ Integral สำหรับชั้นประถมศึกษาปีที่ 9
หนังสือเรียนแบบโต้ตอบสำหรับเกรด 9 "กฎและแบบฝึกหัดทางเรขาคณิต"
หนังสือเรียนอิเล็กทรอนิกส์ "เรขาคณิตที่เข้าใจได้" สำหรับเกรด 7-9

ระบบความไม่เท่าเทียมกัน

พวกคุณคุณได้ศึกษาความไม่เท่าเทียมกันเชิงเส้นและกำลังสองและเรียนรู้วิธีการแก้ปัญหาในหัวข้อเหล่านี้ ทีนี้เรามาดูแนวคิดใหม่ในวิชาคณิตศาสตร์กันดีกว่า - ระบบความไม่เท่าเทียมกัน ระบบอสมการก็คล้ายกับระบบสมการ คุณจำระบบสมการได้ไหม? คุณเรียนระบบสมการตั้งแต่ชั้นประถมศึกษาปีที่ 7 พยายามจำไว้ว่าคุณแก้สมการได้อย่างไร

ให้เราแนะนำคำจำกัดความของระบบความไม่เท่าเทียมกัน
อสมการหลายประการที่มีตัวแปร x บางตัวจะสร้างระบบความไม่เท่าเทียมกันหากคุณต้องการค้นหาค่าทั้งหมดของ x ซึ่งอสมการแต่ละตัวจะสร้างนิพจน์ตัวเลขที่ถูกต้อง

ค่า x ใดๆ ที่แต่ละอสมการใช้นิพจน์ตัวเลขที่ถูกต้องจะเป็นวิธีแก้ปัญหาของอสมการนั้น เรียกได้ว่าเป็นโซลูชันส่วนตัวก็ได้
โซลูชันส่วนตัวคืออะไร? ตัวอย่างเช่น ในคำตอบที่เราได้รับนิพจน์ x>7 จากนั้น x=8 หรือ x=123 หรือจำนวนอื่นๆ ที่มากกว่า 7 จะเป็นคำตอบเฉพาะ และนิพจน์ x>7 จะเป็นคำตอบทั่วไป โซลูชันทั่วไปเกิดขึ้นจากโซลูชันส่วนตัวจำนวนมาก

เรารวมระบบสมการได้อย่างไร? ถูกต้อง วงเล็บปีกกา แล้วพวกมันก็ทำแบบเดียวกันกับอสมการด้วย ลองดูตัวอย่างของระบบความไม่เท่าเทียมกัน: $\begin(cases)x+7>5\\x-3
หากระบบอสมการประกอบด้วยนิพจน์ที่เหมือนกัน เช่น $\begin(cases)x+7>5\\x+7
แล้วมันหมายความว่าอะไร: การค้นหาวิธีแก้ไขระบบความไม่เท่าเทียมกัน?
วิธีแก้ปัญหาความไม่เท่าเทียมกันคือชุดของการแก้ปัญหาบางส่วนสำหรับความไม่เท่าเทียมกันที่ตอบสนองความไม่เท่าเทียมกันของระบบทั้งสองในคราวเดียว

เราเขียนรูปแบบทั่วไปของระบบความไม่เท่าเทียมกันเป็น $\begin(cases)f(x)>0\\g(x)>0\end(cases)$

ให้เราแสดงว่า $XX_1$ เป็นคำตอบทั่วไปของอสมการ f(x)>0
$X_2$ คือคำตอบทั่วไปของอสมการ g(x)>0
$X_1$ และ $X_2$ เป็นชุดของโซลูชันเฉพาะ
วิธีแก้ระบบอสมการคือตัวเลขที่เป็นของทั้ง $X_1$ และ $X_2$
มาจำการดำเนินการกับฉากกัน เราจะค้นหาองค์ประกอบของเซตที่เป็นของทั้งสองเซตพร้อมกันได้อย่างไร? ถูกต้อง มีการดำเนินการทางแยกสำหรับสิ่งนี้ ดังนั้น วิธีแก้อสมการของเราคือเซต $A= X_1∩ X_2$

ตัวอย่างการแก้ปัญหาระบบอสมการ

ลองดูตัวอย่างการแก้ระบบอสมการ

แก้ระบบความไม่เท่าเทียมกัน
a) $\begin(คดี)3x-1>2\\5x-10 b) $\begin(คดี)2x-4≤6\\-x-4
สารละลาย.
ก) แก้ความไม่เท่าเทียมกันแต่ละรายการแยกกัน
$3x-1>2; - 3x>3; - x>1$.
5x-10 ดอลลาร์
ลองทำเครื่องหมายช่วงเวลาของเราบนเส้นพิกัดเส้นเดียว

ผลเฉลยของระบบคือส่วนของจุดตัดของช่วงของเรา ความไม่เท่าเทียมกันนั้นเข้มงวด จากนั้นเซ็กเมนต์จะเปิดขึ้น
คำตอบ: (1;3)

B) เราจะแก้ไขความไม่เท่าเทียมกันแต่ละรายการแยกกัน
$2x-4≤6; 2x≤ 10; x ≤ $5
$-x-4 -5$.


ผลเฉลยของระบบคือส่วนของจุดตัดของช่วงของเรา อสมการที่สองนั้นเข้มงวด จากนั้นส่วนจะเปิดทางด้านซ้าย
คำตอบ: (-5; 5].

มาสรุปสิ่งที่เราได้เรียนรู้กันดีกว่า
สมมติว่าจำเป็นต้องแก้ระบบอสมการ: $\begin(cases)f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end(cases)$
จากนั้น ช่วง ($x_1; x_2$) คือคำตอบของอสมการแรก
ช่วง ($y_1; y_2$) คือคำตอบของอสมการที่สอง
คำตอบของระบบความไม่เท่าเทียมกันคือจุดตัดของคำตอบสำหรับความไม่เท่าเทียมกันแต่ละอย่าง

ระบบความไม่เท่าเทียมกันสามารถประกอบด้วยไม่เพียงแต่ความไม่เท่าเทียมกันลำดับที่หนึ่งเท่านั้น แต่ยังรวมถึงความไม่เท่าเทียมกันประเภทอื่นๆ ด้วย

กฎสำคัญในการแก้ไขระบบอสมการ
ถ้าความไม่เท่าเทียมกันประการใดของระบบไม่มีวิธีแก้ปัญหา แสดงว่าทั้งระบบก็ไม่มีวิธีแก้ปัญหา
ถ้าค่าใดค่าหนึ่งของตัวแปรเป็นไปตามความไม่เท่าเทียมกัน ค่าเฉลยของระบบก็จะเท่ากับค่าเฉลยของค่าอสมการอื่นๆ

ตัวอย่าง.
แก้ระบบอสมการ:$\begin(cases)x^2-16>0\\x^2-8x+12≤0 \end(cases)$
สารละลาย.
มาแก้อสมการแต่ละอันแยกกัน
$x^2-16>0$.
$(x-4)(x+4)>0$.

ลองแก้อสมการที่สองกัน.
$x^2-8x+12≤0$.
$(x-6)(x-2)≤0$.

วิธีแก้อสมการคือช่วงเวลา
ลองวาดทั้งสองช่วงบนเส้นเดียวกันแล้วหาจุดตัดกัน
จุดตัดของช่วงเวลาคือส่วน (4; 6]
คำตอบ: (4;6].

แก้ระบบความไม่เท่าเทียมกัน
a) $\begin(กรณี)3x+3>6\\2x^2+4x+4 b) $\begin(กรณี)3x+3>6\\2x^2+4x+4>0\end(กรณี )$

สารละลาย.
ก) อสมการประการแรกมีทางแก้ x>1
ลองหาตัวจำแนกสำหรับอสมการที่สองกัน
$D=16-4 * 2 * 4=-16$. $D ขอให้เราจำกฎนี้ไว้: เมื่อหนึ่งในอสมการไม่มีวิธีแก้ปัญหา ระบบทั้งหมดก็จะไม่มีทางแก้
คำตอบ: ไม่มีวิธีแก้ปัญหา

B) อสมการแรกมีวิธีแก้ x>1
อสมการที่สองมีค่ามากกว่าศูนย์สำหรับ x ทั้งหมด จากนั้นคำตอบของระบบก็เกิดขึ้นพร้อมกับคำตอบของอสมการแรก
คำตอบ: x>1.

ปัญหาระบบความไม่เท่าเทียมกันเพื่อการแก้ปัญหาอย่างอิสระ

แก้ระบบอสมการ:
a) $\begin(เคส)4x-5>11\\2x-12 b) $\begin(เคส)-3x+1>5\\3x-11 c) $\begin(เคส)x^2-25 d) $\begin(กรณี)x^2-16x+55>0\\x^2-17x+60≥0 \end(กรณี)$
จ) $\begin(กรณี)x^2+36