Графичен метод.. 3

Симплексен метод.. 6

Метод на изкуствена основа... 8

Принципът на дуалността.. 10

Списък на използваната литература... 12

Въведение

Някои свойства на системите от линейни неравенства са разгледани още през първата половина на 19 век във връзка с някои проблеми на аналитичната механика. Систематичното изучаване на системи от линейни неравенства започва в самия край на 19 век, но става възможно да се говори за теория на линейните неравенства едва в края на двадесетте години на 20 век, когато има достатъчен брой резултати, свързани с тях вече натрупани.

Сега теорията на крайните системи от линейни неравенства може да се разглежда като клон на линейната алгебра, произлязъл от нея с допълнителното изискване за подреждане на полето от коефициенти.

Линейните неравенства са особено важни за икономистите, тъй като именно с помощта на линейните неравенства могат да се моделират производствените процеси и да се намерят най-изгодните планове за производство, транспорт, разпределение на ресурси и др.

Тази статия ще очертае основните методи за решаване на линейни неравенства, приложени към конкретни проблеми.

Графичен метод

Графичният метод се състои в конструиране на набор от допустими решения на PLP и намиране в този набор на точката, съответстваща на целевата функция max/min.

Поради ограничените възможности за визуално графично представяне, този метод се използва само за системи от линейни неравенства с две неизвестни и системи, които могат да бъдат редуцирани до този вид.

За да демонстрираме ясно графичния метод, нека решим следния проблем:

На първия етап е необходимо да се изгради област от осъществими решения. За този пример е най-удобно да изберете X2 като абциса и X1 като ордината и да напишете неравенствата в следната форма:

както графиките, така и областта на осъществимите решения са в първото тримесечие.

За да намерим граничните точки, решаваме уравненията (1)=(2), (1)=(3) и (2)=(3).

Както може да се види от илюстрацията, полиедърът ABCDE образува област от възможни решения.

Ако областта на допустимите решения не е затворена, тогава или max(f)=+ ∞, или min(f)= -∞.

Сега можем да продължим директно към намиране на максимума на функцията f.

Чрез алтернативно заместване на координатите на върховете на полиедъра във функцията f и сравняване на стойностите, намираме, че

f(C)=f(4;1)=19 – максимум на функцията.

Този подход е доста полезен с малък брой върхове. Но тази процедура може да отнеме много време, ако има доста върхове.

В този случай е по-удобно да се разглежда линия на ниво от формата f=a. При монотонно нарастване на числото a от -∞ до +∞, правите f=a се изместват по нормалния вектор. Ако при такова движение на линията на нивото има определена точка X - първата обща точка на областта на допустимите решения (многостен ABCDE) и линията на нивото, тогава f(X) е минимумът на f в множеството А Б В Г Д. Ако X е последната точка на пресичане на линията на нивото и множеството ABCDE, тогава f(X) е максимумът на множеството от възможни решения. Ако, като a→-∞, правата f=a пресича множеството от възможни решения, тогава min(f)= -∞. Ако това се случи като a→+∞, тогава

В нашия пример правата f=a пресича областта ABCDE в точка C(4;1). Тъй като това е последната пресечна точка, max(f)=f(C)=f(4;1)=19.

Симплексен метод

Реалните проблеми с линейното програмиране съдържат много голям брой ограничения и неизвестни и се изпълняват на компютър. Симплексният метод е най-общият алгоритъм, използван за решаване на такива проблеми. Същността на метода е, че след определен брой специални симплексни трансформации се разрешава ZLP, намален до специална форма. За да демонстрираме симплексния метод в действие, ще разрешим следния проблем със съпътстващи коментари:

За да започнете да решавате проблем с помощта на симплексния метод, трябва да занесете проблема в специален формуляр и да попълните симплексна таблица.

Система (4) е естествено ограничение и не се вписва в таблицата. Уравнения (1), (2), (3) формират областта на допустимите решения. Израз (5) е целевата функция. Свободните членове в системата от ограничения и областта на допустимите решения трябва да са неотрицателни.

В този пример X3, X4, X5 са основните неизвестни. Те трябва да бъдат изразени чрез свободни неизвестни и заменени в целевата функция.

Сега можете да започнете да попълвате симплексната таблица:

б.	X1	X2	X3	X4	X5	° С
X3	0	-1	1	1	0	1
X4	0	1	-1	0	1	1
X5	1	1	1	0	0	2
f	0	-6	7	0	0	3

Първата колона на тази таблица показва основните неизвестни, последната - стойностите на свободните неизвестни, а останалите - коефициентите на неизвестните.

За да намерите максимума на функцията f, като използвате трансформации на Гаус, трябва да се уверите, че всички коефициенти за неизвестните в последния ред са неотрицателни (за да намерите минимума, уверете се, че всички коефициенти са по-малки или равни до нула).

б	X1	X2	X3	X4	X5	° С
X3	-1	1	1	0	0	1
X4	1	-1	0	1	0	1
X5	1	1	0	0	1	2
f	-6	7	0	0	0	3

За да направите това, изберете колоната с отрицателен коефициент в последния ред (колона 3) и съставете връзката свободен член/коефициент (1/1; 2/1) за положителните елементи на тази колона. От тези съотношения изберете най-малкото и маркирайте съответния ред.

Избрали сме елемента в клетка (3;3). Сега, използвайки метода на Гаус, нулираме други коефициенти в тази колона, това води до промяна в основата и ние сме една стъпка по-близо до оптималното решение.

б	X1	X2	X3	X4	X5	° С
X3	0	0	1	1	0	2
X1	1	-1	0	1	0	1
X5	0	2	0	-1	1	1
f	0	1	0	6	0	9

Както се вижда от таблицата, сега всички коефициенти в последния ред са по-големи или равни на нула. Това означава, че сме намерили оптималната стойност. Свободните неизвестни са равни на нула, стойността на основните неизвестни и максимумът на функцията f съответстват на стойностите на свободните неизвестни.

Нека да разгледаме примери как се решава система от линейни неравенства.

4x + 29 \end(array) \right.\]" title="Изобразено от QuickLaTeX.com">!}

За да решите система, вие се нуждаете от всяко от нейните съставни неравенства. Само решението беше взето да не се пише отделно, а заедно, комбинирайки ги с къдрава скоба.

Във всяко от неравенствата на системата преместваме неизвестните от едната страна, а известните от другата с обратен знак:

Title="Изобразено от QuickLaTeX.com">!}

След опростяването двете страни на неравенството трябва да се разделят на числото пред X. Разделяме първото неравенство на положително число, така че знакът на неравенството не се променя. Разделяме второто неравенство на отрицателно число, така че знакът за неравенство трябва да бъде обърнат:

Title="Изобразено от QuickLaTeX.com">!}

Отбелязваме решението на неравенствата на числовите оси:

В отговор записваме пресечната точка на решенията, тоест частта, където има засенчване на двете линии.

Отговор: x∈[-2;1).

В първото неравенство нека се отървем от дробта. За да направим това, ние умножаваме двете страни член по член по най-малкия общ знаменател 2. Когато се умножи по положително число, знакът за неравенство не се променя.

Във второто неравенство отваряме скобите. Произведението на сбора и разликата на два израза е равно на разликата на квадратите на тези изрази. От дясната страна е квадратът на разликата между двата израза.

Title="Изобразено от QuickLaTeX.com">!}

Преместваме неизвестните от едната страна, известните от другата с обратен знак и опростяваме:

Разделяме двете страни на неравенството на числото пред X. В първото неравенство делим на отрицателно число, така че знакът на неравенството е обърнат. Във втория разделяме на положително число, знакът за неравенство не се променя:

Title="Изобразено от QuickLaTeX.com">!}

И двете неравенства имат знак „по-малко от“ (няма значение, че единият знак е строго „по-малко от“, другият е свободен, „по-малко от или равно“). Не можем да маркираме и двете решения, но използваме правилото “ “. По-малкото е 1, следователно системата се свежда до неравенството

Отбелязваме неговото решение на числовата ос:

Отговор: x∈(-∞;1].

Отваряне на скобите. В първото неравенство - . Тя е равна на сумата от кубовете на тези изрази.

Във втория, произведението на сбора и разликата на два израза, което е равно на разликата на квадратите. Тъй като тук има знак минус пред скобите, по-добре е да ги отворите на два етапа: първо използвайте формулата и едва след това отворете скобите, като промените знака на всеки член на противоположния.

Преместваме неизвестните в една посока, известните в другата с обратен знак:

Title="Изобразено от QuickLaTeX.com">!}

И двете са по-големи от знаци. Използвайки правилото „повече от повече“, свеждаме системата от неравенства до едно неравенство. По-голямото от двете числа е 5, следователно,

Title="Изобразено от QuickLaTeX.com">!}

Отбелязваме решението на неравенството на числовата ос и записваме отговора:

Отговор: x∈(5;∞).

Тъй като в алгебрата системите от линейни неравенства се срещат не само като самостоятелни задачи, но и в процеса на решаване на различни видове уравнения, неравенства и т.н., е важно тази тема да се усвои своевременно.

Следващият път ще разгледаме примери за решаване на системи от линейни неравенства в специални случаи, когато някое от неравенствата няма решения или решението му е произволно число.

Категория: |

Неравенството е две числа или математически изрази, свързани с един от знаците: > (по-голямо от, в случай на строги неравенства),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

Неравенството е линеенпри същите условия като уравнението: то съдържа променливи само на първа степен и не съдържа произведения на променливи.

Решението на линейни неравенства и системи от линейни неравенства е неразривно свързано с тяхното геометрично значение: решението на линейно неравенство е определена полуравнина, на която цялата равнина е разделена от права линия, уравнението на която определя линейното неравенство . Тази полуравнина, а в случай на система от линейни неравенства, частта от равнината, ограничена от няколко прави линии, трябва да се намери на чертежа.

Много икономически проблеми, по-специално проблемите на линейното програмиране, при които се изисква да се намери максимумът или минимумът на функция, се свеждат до решаване на системи от линейни неравенства с голям брой променливи.

Решаване на системи от линейни неравенства с произволен брой неизвестни

Първо, нека разгледаме линейните неравенства в равнината. Помислете за едно неравенство с две променливи и:

,

където са коефициентите на променливите (някои числа), е свободният член (също някакво число).

Едно неравенство с две неизвестни, подобно на уравнение, има безкраен брой решения. Решението на това неравенство е двойка числа, които удовлетворяват това неравенство. Геометрично, наборът от решения на неравенство се изобразява като полуравнина, ограничена от права линия

,

която ще наричаме гранична линия.

Стъпка 1. Построете линия, която ограничава множеството от решения на линейно неравенство

За да направите това, трябва да знаете произволни две точки на тази линия. Нека намерим точките на пресичане с координатните оси. Пресечна ордината Аравна на нула (Фигура 1). Числените стойности на осите на тази фигура се отнасят за пример 1, който ще анализираме веднага след тази теоретична екскурзия.

Намираме абсцисата, като решаваме уравнението на правата с уравнението на оста като система.

Нека намерим пресечната точка с оста:

Като заместим стойността в първото уравнение, получаваме

Където .

Така намерихме абсцисата на точката А .

Нека намерим координатите на пресечната точка с оста.

Абсцисни точки бравно на нула. Нека решим уравнението на граничната линия с уравнението на координатната ос:

,

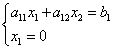
следователно координатите на точката б: .

Стъпка 2. Начертайте права линия, ограничаваща множеството от решения на неравенството.Познаване на точките АИ бпресичане на граничната линия с координатните оси, можем да начертаем тази линия. Права линия (отново Фигура 1) разделя цялата равнина на две части, лежащи отдясно и отляво (отгоре и отдолу) на тази права линия.

Стъпка 3. Определете коя полуравнина е решението на това неравенство.За да направите това, трябва да замените началото на координатите (0; 0) в това неравенство. Ако координатите на началото удовлетворяват неравенството, тогава решението на неравенството е полуравнината, в която се намира началото на координатите. Ако координатите не удовлетворяват неравенството, тогава решението на неравенството е полуравнина, която не съдържа началото. Полуравнината на решението на неравенството ще бъде означена с черти от правата линия в полуравнината, както е на фигура 1.

Ако решим система от линейни неравенства, тогава всяка стъпка се изпълнява за всяко от системните неравенства.

Пример 1.Решете неравенство

Решение. Нека начертаем права линия

Замествайки права линия в уравнението, получаваме , а замествайки , получаваме . Следователно координатите на точките на пресичане с осите ще бъдат А(3; 0) , б(0; 2) . Нека начертаем права линия през тези точки (отново Фигура 1).

Нека изберем полуравнина от решения на неравенството. За да направим това, заместваме координатите на началото (0; 0) в неравенството:

получаваме , т.е. координатите на началото удовлетворяват това неравенство. Следователно решението на неравенството е полуравнината, съдържаща началото на координатите, т.е. лявата (известна още като долна) полуравнина.

Ако това неравенство беше строго, тоест щеше да има формата

тогава точките на граничната линия не биха били решение, тъй като те не удовлетворяват неравенството.

Сега разгледайте система от линейни неравенства с две неизвестни:

Всяко от неравенствата на тази система на равнината определя полуравнина. Система от линейни неравенства се нарича последователна, ако има поне едно решение, и несъгласувана, ако няма решения. Решение на система от линейни неравенства е всяка двойка числа (), която удовлетворява всички неравенства на дадената система.

Геометрично решението на система от линейни неравенства е наборът от точки, които удовлетворяват всички неравенства на системата, тоест общата част на получените полуравнини. Следователно, геометрично, в общия случай, решението може да бъде изобразено под формата на някакъв многоъгълник, в частен случай това може да бъде линия, сегмент или дори точка. Ако една система от линейни неравенства е непоследователна, тогава няма нито една точка на равнината, която да удовлетворява всички неравенства на системата.

Пример 2.

Решение. И така, трябва да намерим многоъгълник от решения на тази система от неравенства. Нека построим гранична линия за първото неравенство, тоест права, и гранична линия за второто неравенство, тоест права.

Правим това стъпка по стъпка, както беше показано в теоретичната справка и в пример 1, особено след като в пример 1 изградихме гранична линия за неравенството, което е първото в тази система.

Полуравнините на решенията, съответстващи на неравенствата на тази система, са защриховани навътре на фигура 2. Общата част на полуравнините на решението е отворен ъгъл ABC. Това означава, че множеството точки в равнината, които образуват отворен ъгъл ABC, е решение както на първото, така и на второто неравенство на системата, т.е. това е решение на система от две линейни неравенства. С други думи, координатите на всяка точка от това множество удовлетворяват и двете неравенства на системата.

Пример 3.Решете система от линейни неравенства

Решение. Нека построим гранични линии, съответстващи на неравенствата на системата. Правим това, като следваме стъпките, дадени в теоретичната помощ за всяко неравенство. Сега определяме полуравнините на решенията за всяко неравенство (Фигура 3).

Полуравнините на решенията, съответстващи на неравенствата на дадена система, са защриховани навътре. Пресечната точка на полуравнини на решения е изобразена, както е показано на фигурата, под формата на четириъгълник ABCE. Открихме, че многоъгълникът от решения на система от линейни неравенства с две променливи е четириъгълник ABCE .

Всичко описано по-горе за системи от линейни неравенства с две неизвестни се отнася и за системи от неравенства с произволен брой неизвестни, с единствената разлика, че решението на неравенството с ннеизвестните ще бъдат съвкупността нчисла (), отговарящи на всички неравенства, и вместо граничната линия ще има гранична хиперравнина н-измерително пространство. Решението ще бъде полиедър на решение (симплекс), ограничен от хиперравнини.

ЛИНЕЙНИ УРАВНЕНИЯ И НЕРАВЕНСТВА I

§ 23 Системи линейни неравенства

Система от линейни неравенства е всеки набор от две или повече линейни неравенства, съдържащи една и съща неизвестна величина.

Примери за такива системи включват следните системи:

Решаването на система от неравенства означава намиране на всички стойности на неизвестното количество, за което всяко неравенство на системата е изпълнено.

Нека решим горните системи.

Нека поставим две числови прави една под друга (фиг. 31); отгоре отбелязваме тези стойности х , за които е изпълнено първото неравенство ( х > 1), а най-отдолу тези стойности х , за които е изпълнено второто неравенство ( х > 4).

Сравнявайки резултатите на числовите прави, забелязваме, че и двете неравенства ще бъдат изпълнени едновременно, когато х > 4. Отговор, х > 4.

Първото неравенство дава -3 х < -б, или х > 2, а вторият - х > -8, или х < 8. Далее поступаем так же, как и в первом примере. На одной числовой прямой отмечаем все те значения х , за които е изпълнено първото неравенство на системата, а на втората числова ос, разположена под първата, всички тези стойности х , за които е изпълнено второто неравенство на системата (фиг. 32).

Сравнението на тези два резултата показва, че и двете неравенства ще са валидни едновременно за всички стойности х , оградени от 2 до 8. Наборът от такива стойности х записано като двойно неравенство 2< х < 8.

Пример 3. Решете системата от неравенства

Първото неравенство на системата дава 5 х < 10, или х < 2, второе х > 4. Следователно всяко число, което удовлетворява и двете неравенства едновременно, трябва да бъде не повече от 2 и повече от 4 (фиг. 33).

Но такива числа не съществуват. Следователно тази система от неравенства не е валидна за никакви стойности х . Такива системи от неравенства се наричат ​​непоследователни.

Упражнения

Решете тези системи от неравенства (№ 179 -184):

Решете неравенства (№ 185, 186):

185. (2х + 3) (2 - 2х ) > 0. 186. (2 - π ) (2х - 15) (х + 4) > 0.

Намерете валидните стойности на буквите, включени в данните за равенство (№ 187, 188):

Решете неравенства (№ 189, 190):

189. 1 < 2х - 5 < 2. 190. -2 < 1 - о < 5.

191. Каква трябва да бъде температурата на 10 литра вода, за да се смеси с 6 литра вода с температура 15°, за да се получи вода с температура най-малко 30° и не повече от 40°?

192. Едната страна на триъгълника е 4 cm, а сборът на другите две е 10 cm. Намерете тези страни, ако са изразени в цели числа.

193. Известно е, че системата от две линейни неравенства не е изпълнена за никакви стойности на неизвестното количество. Можем ли да кажем, че отделните неравенства на тази система не са изпълнени за никакви стойности на неизвестното количество?

Допълнителни материали
Уважаеми потребители, не забравяйте да оставите вашите коментари, отзиви, пожелания! Всички материали са проверени с антивирусна програма.

Учебни помагала и тренажори в онлайн магазина Интеграл за 9 клас
Интерактивен учебник за 9 клас "Правила и упражнения по геометрия"
Електронен учебник "Разбираема геометрия" за 7-9 клас

Система от неравенства

Момчета, вие изучавахте линейни и квадратни неравенства и се научихте как да решавате задачи по тези теми. Сега да преминем към едно ново понятие в математиката - система от неравенства. Система от неравенства е подобна на система от уравнения. Спомняте ли си системи от уравнения? Учили сте системи уравнения в седми клас, опитайте се да си спомните как сте ги решили.

Нека въведем определението за система от неравенства.
Няколко неравенства с някаква променлива x образуват система от неравенства, ако трябва да намерите всички стойности на x, за които всяко от неравенствата образува правилен числов израз.

Всяка стойност на x, за която всяко неравенство приема правилния цифров израз, е решение на неравенството. Може да се нарече и частно решение.
Какво е частно решение? Например в отговора получихме израза x>7. Тогава x=8, или x=123, или всяко друго число, по-голямо от седем, е конкретно решение, а изразът x>7 е общо решение. Общото решение се формира от много частни решения.

Как комбинирахме системата от уравнения? Точно така, къдрава скоба и те правят същото с неравенствата. Нека да разгледаме пример за система от неравенства: $\begin(cases)x+7>5\\x-3
Ако системата от неравенства се състои от еднакви изрази, например $\begin(cases)x+7>5\\x+7
И така, какво означава: да се намери решение на система от неравенства?
Решение на неравенство е набор от частични решения на неравенство, които удовлетворяват едновременно и двете неравенства на системата.

Записваме общата форма на системата от неравенства като $\begin(cases)f(x)>0\\g(x)>0\end(cases)$

Нека обозначим $Х_1$ като общо решение на неравенството f(x)>0.
$X_2$ е общото решение на неравенството g(x)>0.
$X_1$ и $X_2$ са набор от конкретни решения.
Решението на системата от неравенства ще бъдат числа, принадлежащи както на $X_1$, така и на $X_2$.
Нека си припомним операциите върху множества. Как да намерим елементи от множество, които принадлежат на двете множества едновременно? Точно така, има операция за пресичане за това. И така, решението на нашето неравенство ще бъде множеството $A= X_1∩ X_2$.

Примери за решения на системи от неравенства

Нека да разгледаме примери за решаване на системи от неравенства.

Решете системата от неравенства.
a) $\begin(cases)3x-1>2\\5x-10 b) $\begin(cases)2x-4≤6\\-x-4
Решение.
а) Решете всяко неравенство поотделно.
$3x-1>2; \; 3x>3; \; x>1$.
$5x-10
Нека отбележим нашите интервали на една координатна линия.

Решението на системата ще бъде сегментът на пресичане на нашите интервали. Неравенството е строго, тогава сегментът ще бъде отворен.
Отговор: (1;3).

Б) Освен това ще решим всяко неравенство поотделно.
$2x-4≤6; 2x≤ 10; x ≤ $5.
$-x-4 -5$.


Решението на системата ще бъде сегментът на пресичане на нашите интервали. Второто неравенство е строго, тогава сегментът ще бъде отворен отляво.
Отговор: (-5; 5].

Нека обобщим наученото.
Да приемем, че е необходимо да се реши системата от неравенства: $\begin(cases)f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end(cases)$.
Тогава интервалът ($x_1; x_2$) е решението на първото неравенство.
Интервалът ($y_1; y_2$) е решението на второто неравенство.
Решението на система от неравенства е пресечната точка на решенията на всяко неравенство.

Системите от неравенства могат да се състоят не само от неравенства от първи ред, но и от всякакви други видове неравенства.

Важни правила за решаване на системи от неравенства.
Ако едно от неравенствата на системата няма решения, то цялата система няма решения.
Ако едно от неравенствата е изпълнено за всякакви стойности на променливата, тогава решението на системата ще бъде решението на другото неравенство.

Примери.
Решете системата от неравенства:$\begin(cases)x^2-16>0\\x^2-8x+12≤0 \end(cases)$
Решение.
Нека решим всяко неравенство поотделно.
$x^2-16>0$.
$(x-4)(x+4)>0$.

Нека решим второто неравенство.
$x^2-8x+12≤0$.
$(x-6)(x-2)≤0$.

Решението на неравенството е интервалът.
Нека начертаем двата интервала на една права и да намерим пресечната точка.
Пресечната точка на интервалите е отсечката (4; 6).
Отговор: (4;6].

Решете системата от неравенства.
a) $\begin(cases)3x+3>6\\2x^2+4x+4 b) $\begin(cases)3x+3>6\\2x^2+4x+4>0\end(cases )$.

Решение.
а) Първото неравенство има решение x>1.
Нека намерим дискриминанта за второто неравенство.
$D=16-4 * 2 * 4=-16$. $D Нека си припомним правилото: когато едно от неравенствата няма решения, то цялата система няма решения.
Отговор: Няма решения.

Б) Първото неравенство има решение x>1.
Второто неравенство е по-голямо от нула за всички x. Тогава решението на системата съвпада с решението на първото неравенство.
Отговор: x>1.

Задачи от системи неравенства за самостоятелно решаване

Решете системи от неравенства:
a) $\begin(cases)4x-5>11\\2x-12 b) $\begin(cases)-3x+1>5\\3x-11 c) $\begin(cases)x^2-25 г) $\begin(cases)x^2-16x+55>0\\x^2-17x+60≥0 \end(cases)$
д) $\begin(cases)x^2+36