ग्राफ़िक विधि..3

सरल विधि ।।6।

कृत्रिम आधार विधि...8

द्वैत का सिद्धांत।।10।

प्रयुक्त साहित्य की सूची...12

परिचय

विश्लेषणात्मक यांत्रिकी की कुछ समस्याओं के संबंध में 19वीं शताब्दी के पूर्वार्द्ध में रैखिक असमानताओं की प्रणालियों के कुछ गुणों पर विचार किया गया था। रैखिक असमानताओं की प्रणालियों का व्यवस्थित अध्ययन 19वीं शताब्दी के अंत में शुरू हुआ, लेकिन रैखिक असमानताओं के सिद्धांत के बारे में बात करना 20वीं शताब्दी के उत्तरार्ध में ही संभव हो सका, जब उनसे संबंधित पर्याप्त संख्या में परिणाम सामने आए। पहले ही जमा हो चुका है.

अब रैखिक असमानताओं की परिमित प्रणालियों के सिद्धांत को रैखिक बीजगणित की एक शाखा के रूप में माना जा सकता है, जो गुणांक के क्षेत्र को क्रमबद्ध करने की अतिरिक्त आवश्यकता के साथ विकसित हुई है।

अर्थशास्त्रियों के लिए रैखिक असमानताएँ विशेष रूप से महत्वपूर्ण हैं, क्योंकि यह रैखिक असमानताओं की मदद से है कि कोई उत्पादन प्रक्रियाओं को मॉडल कर सकता है और उत्पादन, परिवहन, संसाधनों के आवंटन आदि के लिए सबसे लाभदायक योजनाएँ पा सकता है।

यह पेपर विशिष्ट समस्याओं पर लागू रैखिक असमानताओं को हल करने के लिए बुनियादी तरीकों की रूपरेखा तैयार करेगा।

ग्राफ़िकल विधि

ग्राफ़िकल विधि में पीएलपी के लिए स्वीकार्य समाधानों का एक सेट बनाना और इसमें अधिकतम/न्यूनतम उद्देश्य फ़ंक्शन के अनुरूप बिंदु ढूंढना शामिल है।

दृश्य ग्राफिक प्रतिनिधित्व की सीमित संभावनाओं के कारण, इस पद्धति का उपयोग केवल दो अज्ञात और सिस्टम के साथ रैखिक असमानताओं की प्रणालियों के लिए किया जाता है जिन्हें इस रूप में कम किया जा सकता है।

ग्राफिकल विधि को स्पष्ट रूप से प्रदर्शित करने के लिए, आइए निम्नलिखित समस्या को हल करें:

पहले चरण में, व्यवहार्य समाधानों का एक क्षेत्र बनाना आवश्यक है। इस उदाहरण के लिए, भुज के रूप में X2 और कोटि के रूप में X1 का चयन करना और असमानताओं को निम्नलिखित रूप में लिखना सबसे सुविधाजनक है:

ग्राफ़ और व्यवहार्य समाधान का क्षेत्र दोनों पहली तिमाही में हैं।

सीमा बिंदु खोजने के लिए, हम समीकरण (1)=(2), (1)=(3) और (2)=(3) हल करते हैं।

जैसा कि चित्रण से देखा जा सकता है, बहुफलक ABCDE व्यवहार्य समाधानों का एक क्षेत्र बनाता है।

यदि व्यवहार्य समाधान का क्षेत्र बंद नहीं है, तो या तो max(f)=+ ∞ या min(f)= -∞.

अब हम सीधे फलन f का अधिकतम ज्ञात करने के लिए आगे बढ़ सकते हैं।

फ़ंक्शन f में बहुफलक के शीर्षों के निर्देशांकों को बारी-बारी से प्रतिस्थापित करके और मानों की तुलना करके, हम पाते हैं कि

f(C)=f(4;1)=19 - फ़ंक्शन का अधिकतम।

यह दृष्टिकोण कम संख्या में शीर्षों के साथ काफी लाभदायक है। लेकिन यदि बहुत सारे शीर्ष हों तो इस प्रक्रिया में लंबा समय लग सकता है।

इस मामले में, f=a के रूप की एक स्तर रेखा पर विचार करना अधिक सुविधाजनक है। संख्या a में -∞ से +∞ तक एक मोनोटोनिक वृद्धि के साथ, सीधी रेखाएं f=सामान्य वेक्टर के साथ शिफ्ट हो जाती हैं। यदि, स्तर रेखा के इस तरह के आंदोलन के साथ, एक निश्चित बिंदु एबीसीडीई। यदि X स्तर रेखा और ABCDE सेट के प्रतिच्छेदन का अंतिम बिंदु है, तो संभव समाधानों के सेट पर f(X) अधिकतम है। यदि, a→-∞ के रूप में, सीधी रेखा f=a व्यवहार्य समाधानों के सेट को काटती है, तो min(f)= -∞। यदि यह a→+∞ के रूप में होता है, तो

हमारे उदाहरण में, सीधी रेखा f=a क्षेत्रफल ABCDE को बिंदु C(4;1) पर काटती है। चूँकि यह अंतिम प्रतिच्छेदन बिंदु है, max(f)=f(C)=f(4;1)=19.

सिम्प्लेक्स विधि

वास्तविक रैखिक प्रोग्रामिंग समस्याओं में बहुत बड़ी संख्या में बाधाएं और अज्ञात होते हैं और इन्हें कंप्यूटर पर निष्पादित किया जाता है। ऐसी समस्याओं को हल करने के लिए सिंप्लेक्स विधि सबसे सामान्य एल्गोरिदम है। विधि का सार यह है कि एक निश्चित संख्या में विशेष सिम्प्लेक्स परिवर्तनों के बाद, ZLP, एक विशेष रूप में कम हो जाता है, हल हो जाता है। सिम्पलेक्स विधि को क्रियान्वित करने के लिए, आइए हम टिप्पणियों के साथ निम्नलिखित समस्या का समाधान करें:

सिंप्लेक्स विधि द्वारा समस्या को हल करना शुरू करने के लिए, आपको समस्या को एक विशेष फॉर्म में लाना होगा और सिंप्लेक्स तालिका को भरना होगा।

सिस्टम (4) एक प्राकृतिक सीमा है और तालिका में फिट नहीं बैठता है। समीकरण (1), (2), (3) व्यवहार्य समाधान का क्षेत्र बनाते हैं। अभिव्यक्ति (5) वस्तुनिष्ठ फलन है। प्रतिबंधों की प्रणाली और स्वीकार्य समाधानों के क्षेत्र में मुक्त शर्तें गैर-नकारात्मक होनी चाहिए।

इस उदाहरण में, X3, X4, X5 मूल अज्ञात हैं। उन्हें मुक्त अज्ञात के रूप में व्यक्त किया जाना चाहिए और उद्देश्य फ़ंक्शन में प्रतिस्थापित किया जाना चाहिए।

अब आप सिंप्लेक्स तालिका भरना शुरू कर सकते हैं:

बी।	X1	एक्स2	एक्स3	एक्स4	X5	सी
एक्स3	0	-1	1	1	0	1
एक्स4	0	1	-1	0	1	1
X5	1	1	1	0	0	2
एफ	0	-6	7	0	0	3

इस तालिका का पहला कॉलम मूल अज्ञात को इंगित करता है, अंतिम - मुक्त अज्ञात के मान, और बाकी - अज्ञात के गुणांक।

फ़ंक्शन f का अधिकतम पता लगाने के लिए, गाऊसी परिवर्तनों का उपयोग करते हुए, आपको यह सुनिश्चित करना होगा कि अंतिम पंक्ति में अज्ञात के लिए सभी गुणांक गैर-नकारात्मक हैं (न्यूनतम खोजने के लिए, सुनिश्चित करें कि सभी गुणांक इससे कम या बराबर हैं शून्य तक)।

बी	X1	एक्स2	एक्स3	एक्स4	X5	सी
एक्स3	-1	1	1	0	0	1
एक्स4	1	-1	0	1	0	1
X5	1	1	0	0	1	2
एफ	-6	7	0	0	0	3

ऐसा करने के लिए, अंतिम पंक्ति (स्तंभ 3) में ऋणात्मक गुणांक वाले स्तंभ का चयन करें और इस स्तंभ के सकारात्मक तत्वों के लिए मुक्त पद/गुणांक संबंध (1/1; 2/1) बनाएं। इन अनुपातों में से सबसे छोटे अनुपात का चयन करें और संबंधित रेखा को चिह्नित करें।

हमने सेल (3;3) में तत्व का चयन किया है। अब, गॉसियन विधि का उपयोग करके, हम इस कॉलम में अन्य गुणांकों को रीसेट करते हैं, इससे आधार में बदलाव होता है और हम इष्टतम समाधान के एक कदम करीब हैं।

बी	X1	एक्स2	एक्स3	एक्स4	X5	सी
एक्स3	0	0	1	1	0	2
X1	1	-1	0	1	0	1
X5	0	2	0	-1	1	1
एफ	0	1	0	6	0	9

जैसा कि तालिका से देखा जा सकता है, अब अंतिम पंक्ति के सभी गुणांक शून्य से अधिक या उसके बराबर हैं। इसका मतलब है कि हमें इष्टतम मूल्य मिल गया है। मुक्त अज्ञात शून्य के बराबर हैं, मूल अज्ञात का मान और फ़ंक्शन f का अधिकतम मान मुक्त अज्ञात के मान के अनुरूप है।

आइए रैखिक असमानताओं की प्रणाली को कैसे हल करें इसके उदाहरण देखें।

4x + 29 \end(array) \right.\]" title='QuickLaTeX.com द्वारा प्रस्तुत">!}

किसी प्रणाली को हल करने के लिए, आपको इसकी प्रत्येक घटक असमानताओं की आवश्यकता होती है। केवल यह निर्णय लिया गया कि अलग-अलग नहीं लिखा जाए, बल्कि एक साथ, उन्हें एक घुंघराले ब्रेस के साथ जोड़ा जाए।

सिस्टम की प्रत्येक असमानता में, हम विपरीत चिह्न के साथ अज्ञात को एक तरफ और ज्ञात को दूसरी तरफ ले जाते हैं:

शीर्षक='QuickLaTeX.com द्वारा प्रस्तुत">!}

सरलीकरण के बाद असमानता के दोनों पक्षों को X के सामने वाली संख्या से विभाजित किया जाना चाहिए। हम पहली असमानता को एक धनात्मक संख्या से विभाजित करते हैं, इसलिए असमानता का चिह्न नहीं बदलता है। हम दूसरी असमानता को एक ऋणात्मक संख्या से विभाजित करते हैं, इसलिए असमानता का चिह्न उलटा होना चाहिए:

शीर्षक='QuickLaTeX.com द्वारा प्रस्तुत">!}

हम संख्या रेखाओं पर असमानताओं के समाधान को चिह्नित करते हैं:

जवाब में, हम समाधानों के प्रतिच्छेदन को लिखते हैं, यानी वह हिस्सा जहां दोनों रेखाओं पर छायांकन होता है।

उत्तर: x∈[-2;1).

पहली असमानता में, आइए भिन्न से छुटकारा पाएं। ऐसा करने के लिए, हम दोनों पक्षों को पद दर पद न्यूनतम उभयनिष्ठ हर 2 से गुणा करते हैं। जब किसी धनात्मक संख्या से गुणा किया जाता है, तो असमानता चिह्न नहीं बदलता है।

दूसरी असमानता में हम कोष्ठक खोलते हैं। दो भावों के योग और अंतर का गुणनफल इन भावों के वर्गों के अंतर के बराबर होता है। दाहिनी ओर दोनों भावों के बीच अंतर का वर्ग है।

शीर्षक='QuickLaTeX.com द्वारा प्रस्तुत">!}

हम विपरीत चिह्न के साथ अज्ञात को एक ओर और ज्ञात को दूसरी ओर ले जाते हैं और सरल बनाते हैं:

हम असमानता के दोनों पक्षों को X के सामने वाली संख्या से विभाजित करते हैं। पहली असमानता में, हम एक ऋणात्मक संख्या से विभाजित करते हैं, इसलिए असमानता का चिह्न उलट जाता है। दूसरे में, हम एक धनात्मक संख्या से विभाजित करते हैं, असमानता का चिह्न नहीं बदलता है:

शीर्षक='QuickLaTeX.com द्वारा प्रस्तुत">!}

दोनों असमानताओं में "इससे कम" चिह्न है (इससे कोई फर्क नहीं पड़ता कि एक चिह्न सख्ती से "इससे कम" है, दूसरा ढीला है, "इससे कम या बराबर")। हम दोनों समाधानों को चिह्नित नहीं कर सकते, लेकिन " " नियम का उपयोग कर सकते हैं। छोटा वाला 1 है, इसलिए सिस्टम असमानता को कम कर देता है

हम इसका हल संख्या रेखा पर अंकित करते हैं:

उत्तर: x∈(-∞;1].

कोष्ठक खोलना. पहली असमानता में - . यह इन भावों के घनों के योग के बराबर है।

दूसरे में, दो भावों के योग और अंतर का गुणनफल, जो वर्गों के अंतर के बराबर है। चूँकि यहाँ कोष्ठक के सामने ऋण चिह्न है, इसलिए उन्हें दो चरणों में खोलना बेहतर है: पहले सूत्र का उपयोग करें, और उसके बाद ही प्रत्येक पद के चिह्न को विपरीत में बदलते हुए कोष्ठक खोलें।

हम अज्ञात को एक दिशा में ले जाते हैं, ज्ञात को विपरीत संकेत के साथ दूसरी दिशा में:

शीर्षक='QuickLaTeX.com द्वारा प्रस्तुत">!}

दोनों लक्षण से भी बढ़कर हैं. "अधिक से अधिक" नियम का उपयोग करके, हम असमानताओं की प्रणाली को एक असमानता तक कम कर देते हैं। दोनों संख्याओं में से बड़ी संख्या 5 है, इसलिए,

शीर्षक='QuickLaTeX.com द्वारा प्रस्तुत">!}

हम असमानता के समाधान को संख्या रेखा पर चिह्नित करते हैं और उत्तर लिखते हैं:

उत्तर: x∈(5;∞).

चूँकि बीजगणित में रैखिक असमानताओं की प्रणालियाँ न केवल स्वतंत्र कार्यों के रूप में होती हैं, बल्कि विभिन्न प्रकार के समीकरणों, असमानताओं आदि को हल करने के दौरान भी होती हैं, इसलिए इस विषय पर समय रहते महारत हासिल करना महत्वपूर्ण है।

अगली बार हम विशेष मामलों में रैखिक असमानताओं की प्रणालियों को हल करने के उदाहरण देखेंगे जब असमानताओं में से किसी एक का कोई समाधान नहीं है या इसका समाधान कोई संख्या है।

श्रेणी: |

असमानता दो संख्याएँ या गणितीय अभिव्यक्तियाँ हैं जो किसी एक संकेत से जुड़ी होती हैं: > (सख्त असमानताओं के मामले में, इससे अधिक),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

असमानता है रेखीयसमीकरण के समान शर्तों के तहत: इसमें केवल पहली डिग्री तक चर होते हैं और चर के उत्पाद शामिल नहीं होते हैं।

रैखिक असमानताओं और रैखिक असमानताओं की प्रणालियों का समाधान उनके ज्यामितीय अर्थ के साथ अटूट रूप से जुड़ा हुआ है: एक रैखिक असमानता का समाधान एक निश्चित अर्ध-तल है जिसमें संपूर्ण तल एक सीधी रेखा से विभाजित होता है, जिसका समीकरण रैखिक असमानता को परिभाषित करता है . यह अर्ध-तल, और रैखिक असमानताओं की प्रणाली के मामले में, कई सीधी रेखाओं द्वारा सीमित विमान का हिस्सा, ड्राइंग में पाया जाना चाहिए।

कई आर्थिक समस्याएं, विशेष रूप से, रैखिक प्रोग्रामिंग समस्याएं, जिनमें किसी फ़ंक्शन का अधिकतम या न्यूनतम पता लगाना आवश्यक होता है, बड़ी संख्या में चर के साथ रैखिक असमानताओं की प्रणालियों को हल करने के लिए कम हो जाती हैं।

किसी भी संख्या में अज्ञात के साथ रैखिक असमानताओं की प्रणालियों को हल करना

सबसे पहले, आइए समतल में रैखिक असमानताओं को देखें। दो चर वाली एक असमानता पर विचार करें और:

,

चरों के गुणांक (कुछ संख्याएँ) कहाँ हैं, मुक्त पद (कुछ संख्याएँ भी) हैं।

दो अज्ञातों वाली एक असमानता, एक समीकरण की तरह, अनंत संख्या में समाधानों वाली होती है। इस असमानता का समाधान संख्याओं की एक जोड़ी है जो इस असमानता को संतुष्ट करती है। ज्यामितीय रूप से, असमानता के समाधान के सेट को एक सीधी रेखा से घिरे आधे-तल के रूप में दर्शाया गया है

,

जिसे हम सीमा रेखा कहेंगे.

चरण 1. एक रैखिक असमानता के समाधानों के सेट को सीमित करने वाली एक सीधी रेखा का निर्माण करें

ऐसा करने के लिए, आपको इस लाइन पर किन्हीं दो बिंदुओं को जानना होगा। आइए निर्देशांक अक्षों के साथ प्रतिच्छेदन बिंदु ज्ञात करें। प्रतिच्छेदन समन्वय एशून्य के बराबर (चित्र 1)। इस चित्र में अक्षों पर संख्यात्मक मान उदाहरण 1 को संदर्भित करते हैं, जिसका विश्लेषण हम इस सैद्धांतिक भ्रमण के तुरंत बाद करेंगे।

हम एक प्रणाली के रूप में अक्ष के समीकरण के साथ सीधी रेखा के समीकरण को हल करके भुज का पता लगाते हैं।

आइए अक्ष के साथ प्रतिच्छेदन खोजें:

मान को पहले समीकरण में प्रतिस्थापित करने पर, हमें प्राप्त होता है

कहाँ ।

इस प्रकार, हमने बिंदु का भुज पाया ए .

आइए अक्ष के साथ प्रतिच्छेदन बिंदु के निर्देशांक ज्ञात करें।

एब्सिस्सा बिंदु बीशून्य के बराबर. आइए हम निर्देशांक अक्ष के समीकरण के साथ सीमा रेखा के समीकरण को हल करें:

,

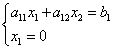
इसलिए, बिंदु के निर्देशांक बी: .

चरण 2. असमानता के समाधानों के सेट को सीमित करने वाली एक सीधी रेखा खींचें।बिन्दुओं को जानना एऔर बीनिर्देशांक अक्षों के साथ सीमा रेखा का प्रतिच्छेदन, हम यह रेखा खींच सकते हैं। एक सीधी रेखा (फिर से चित्र 1) पूरे तल को इस सीधी रेखा के दाएं और बाएं (ऊपर और नीचे) दो भागों में विभाजित करती है।

चरण 3. निर्धारित करें कि कौन सा अर्ध-तल इस असमानता का समाधान है।ऐसा करने के लिए, आपको इस असमानता में निर्देशांक की उत्पत्ति (0; 0) को प्रतिस्थापित करना होगा। यदि मूल के निर्देशांक असमानता को संतुष्ट करते हैं, तो असमानता का समाधान वह आधा तल है जिसमें मूल स्थित है। यदि निर्देशांक असमानता को संतुष्ट नहीं करते हैं, तो असमानता का समाधान एक आधा-तल है जिसमें मूल शामिल नहीं है। असमानता के समाधान के आधे तल को सीधी रेखा से आधे तल में स्ट्रोक द्वारा दर्शाया जाएगा, जैसा कि चित्र 1 में दिखाया गया है।

यदि हम रैखिक असमानताओं की एक प्रणाली को हल करते हैं, फिर प्रत्येक चरण सिस्टम की प्रत्येक असमानता के लिए किया जाता है।

उदाहरण 1।असमानता का समाधान करें

समाधान। चलिए एक सीधी रेखा खींचते हैं

समीकरण में एक सीधी रेखा प्रतिस्थापित करने पर, हमें प्राप्त होता है, और प्रतिस्थापित करने पर, हमें प्राप्त होता है। इसलिए, अक्षों के साथ प्रतिच्छेदन बिंदुओं के निर्देशांक होंगे ए(3; 0) , बी(0; 2) . आइए इन बिंदुओं से होकर एक सीधी रेखा खींचें (फिर से, चित्र 1)।

आइए हम असमानता के समाधान का एक आधा-स्तर चुनें। ऐसा करने के लिए, हम मूल के निर्देशांक (0; 0) को असमानता में प्रतिस्थापित करते हैं:

हम प्राप्त करते हैं, अर्थात मूल के निर्देशांक इस असमानता को संतुष्ट करते हैं। नतीजतन, असमानता का समाधान अर्ध-तल है जिसमें निर्देशांक की उत्पत्ति होती है, यानी, बायां (उर्फ निचला) आधा-तल।

यदि यह असमानता कठोर होती, अर्थात् इसका स्वरूप होता

तब सीमा रेखा के बिंदु कोई समाधान नहीं होंगे, क्योंकि वे असमानता को संतुष्ट नहीं करते हैं।

अब दो अज्ञात के साथ रैखिक असमानताओं की एक प्रणाली पर विचार करें:

समतल पर इस प्रणाली की प्रत्येक असमानता एक अर्ध-तल को परिभाषित करती है। रैखिक असमानताओं की एक प्रणाली को सुसंगत कहा जाता है यदि इसका कम से कम एक समाधान हो, और असंगत कहा जाता है यदि इसका कोई समाधान नहीं है। रैखिक असमानताओं की प्रणाली का समाधान संख्याओं का कोई भी युग्म () है जो दी गई प्रणाली की सभी असमानताओं को संतुष्ट करता है।

ज्यामितीय रूप से, रैखिक असमानताओं की एक प्रणाली का समाधान उन बिंदुओं का समूह है जो प्रणाली की सभी असमानताओं को संतुष्ट करता है, अर्थात, परिणामी अर्ध-तलों का सामान्य भाग। इसलिए, ज्यामितीय रूप से, सामान्य मामले में, समाधान को किसी विशेष मामले में कुछ बहुभुज के रूप में दर्शाया जा सकता है, यह एक रेखा, एक खंड या एक बिंदु भी हो सकता है; यदि रैखिक असमानताओं की एक प्रणाली असंगत है, तो विमान पर एक भी बिंदु ऐसा नहीं है जो प्रणाली की सभी असमानताओं को संतुष्ट करता हो।

उदाहरण 2.

समाधान। इसलिए, हमें असमानताओं की इस प्रणाली के समाधान का एक बहुभुज खोजने की आवश्यकता है। आइए पहली असमानता के लिए एक सीमा रेखा, यानी एक रेखा, और दूसरी असमानता के लिए एक सीमा रेखा, यानी एक रेखा का निर्माण करें।

हम इसे चरण दर चरण करते हैं, जैसा कि सैद्धांतिक संदर्भ और उदाहरण 1 में दिखाया गया था, खासकर जब से उदाहरण 1 में हमने असमानता के लिए एक सीमा रेखा बनाई है, जो इस प्रणाली में पहली है।

इस प्रणाली की असमानताओं के अनुरूप समाधानों के आधे तल चित्र 2 में अंदर की ओर छायांकित हैं। समाधान अर्ध-तल का सामान्य भाग एक खुला कोण है एबीसी. इसका मतलब है कि विमान में बिंदुओं का समूह जो एक खुला कोण बनाता है एबीसी, प्रणाली की पहली और दूसरी दोनों असमानताओं का समाधान है, अर्थात यह दो रैखिक असमानताओं की प्रणाली का समाधान है। दूसरे शब्दों में, इस सेट से किसी भी बिंदु के निर्देशांक प्रणाली की दोनों असमानताओं को संतुष्ट करते हैं।

उदाहरण 3.रैखिक असमानताओं की एक प्रणाली को हल करें

समाधान। आइए हम प्रणाली की असमानताओं के अनुरूप सीमा रेखाएं बनाएं। हम प्रत्येक असमानता के लिए सैद्धांतिक सहायता में दिए गए चरणों का पालन करके ऐसा करते हैं। अब हम प्रत्येक असमानता के लिए समाधान के अर्ध-तल निर्धारित करते हैं (चित्र 3)।

किसी दिए गए सिस्टम की असमानताओं के अनुरूप समाधानों के आधे-तलों को अंदर की ओर छायांकित किया जाता है। जैसा कि चित्र में दिखाया गया है, समाधानों के आधे-तलों के प्रतिच्छेदन को एक चतुर्भुज के रूप में दर्शाया गया है एबीसीई. हमने पाया कि दो चर वाली रैखिक असमानताओं की प्रणाली के समाधान का बहुभुज एक चतुर्भुज है एबीसीई .

दो अज्ञात के साथ रैखिक असमानताओं की प्रणालियों के बारे में ऊपर वर्णित सभी चीजें किसी भी संख्या में अज्ञात के साथ असमानताओं की प्रणालियों पर भी लागू होती हैं, एकमात्र अंतर यह है कि असमानता का समाधान एनअज्ञात ही समग्रता होगी एनसंख्याएँ () सभी असमानताओं को संतुष्ट करती हैं, और सीमा रेखा के बजाय एक सीमा हाइपरप्लेन होगी एन-आयामी स्थान. समाधान हाइपरप्लेन से घिरा एक समाधान पॉलीहेड्रॉन (सिंप्लेक्स) होगा।

रैखिक समीकरण और असमानताएँ I

§ 23 रैखिक असमानताओं की प्रणालियाँ

रैखिक असमानताओं की एक प्रणाली दो या दो से अधिक रैखिक असमानताओं का एक सेट है जिसमें समान अज्ञात मात्रा होती है।

ऐसी प्रणालियों के उदाहरणों में निम्नलिखित प्रणालियाँ शामिल हैं:

असमानताओं की एक प्रणाली को हल करने का अर्थ है अज्ञात मात्रा के सभी मान ज्ञात करना जिसके लिए प्रणाली की प्रत्येक असमानता संतुष्ट होती है।

आइए उपरोक्त प्रणालियों को हल करें।

आइए दो संख्या रेखाओं को एक के नीचे एक रखें (चित्र 31); शीर्ष पर हम उन मूल्यों को चिह्नित करते हैं एक्स , जिसके लिए पहली असमानता संतुष्ट है ( एक्स > 1), और सबसे नीचे वे मान एक्स , जिसके लिए दूसरी असमानता संतुष्ट है ( एक्स > 4).

संख्या रेखाओं पर परिणामों की तुलना करने पर, हम देखते हैं कि दोनों असमानताएँ एक साथ कब संतुष्ट होंगी एक्स > 4. उत्तर, एक्स > 4.

पहली असमानता -3 देती है एक्स < -б, или एक्स > 2, और दूसरा - एक्स >-8, या एक्स < 8. Далее поступаем так же, как и в первом примере. На одной числовой прямой отмечаем все те значения एक्स , जिसके लिए सिस्टम की पहली असमानता संतुष्ट है, और दूसरी संख्या रेखा पर, पहले के नीचे स्थित, वे सभी मान एक्स , जिसके लिए सिस्टम की दूसरी असमानता संतुष्ट है (चित्र 32)।

इन दोनों परिणामों की तुलना से पता चलता है कि दोनों असमानताएं सभी मूल्यों के लिए एक साथ लागू होंगी एक्स , 2 से 8 तक संलग्न। ऐसे मानों का समुच्चय एक्स दोहरी असमानता 2 के रूप में लिखा गया< एक्स < 8.

उदाहरण 3. असमानताओं की प्रणाली को हल करें

सिस्टम की पहली असमानता 5 देती है एक्स < 10, или एक्स < 2, второе एक्स > 4. इस प्रकार, कोई भी संख्या जो दोनों असमानताओं को एक साथ संतुष्ट करती है, 2 से अधिक और 4 से अधिक नहीं होनी चाहिए (चित्र 33)।

लेकिन ऐसे नंबर मौजूद नहीं हैं. इसलिए, असमानताओं की यह प्रणाली किसी भी मूल्य पर आधारित नहीं है एक्स . असमानताओं की ऐसी प्रणालियों को असंगत कहा जाता है।

अभ्यास

असमानताओं की इन प्रणालियों को हल करें (संख्या 179 -184):

असमानताओं को हल करें (संख्या 185, 186):

185. (2एक्स + 3) (2 - 2एक्स ) > 0. 186. (2 - π ) (2एक्स - 15) (एक्स + 4) > 0.

समानता डेटा (संख्या 187, 188) में शामिल अक्षरों के वैध मान ज्ञात करें:

असमानताओं को हल करें (संख्या 189, 190):

189. 1 < 2एक्स - 5 < 2. 190. -2 < 1 - ओह < 5.

191. कम से कम 30° और 40° से अधिक तापमान वाला पानी प्राप्त करने के लिए 15° के तापमान पर 6 लीटर पानी के साथ मिलाने के लिए 10 लीटर पानी का तापमान क्या होना चाहिए?

192. त्रिभुज की एक भुजा 4 सेमी है, और अन्य दो भुजाओं का योग 10 सेमी है। यदि इन्हें पूर्णांकों में व्यक्त किया जाए तो इन भुजाओं का योग ज्ञात कीजिए।

193. यह ज्ञात है कि दो रैखिक असमानताओं की प्रणाली अज्ञात मात्रा के किसी भी मान के लिए संतुष्ट नहीं है। क्या हम कह सकते हैं कि इस प्रणाली की व्यक्तिगत असमानताएँ अज्ञात मात्रा के किसी भी मान से संतुष्ट नहीं हैं?

अतिरिक्त सामग्री
प्रिय उपयोगकर्ताओं, अपनी टिप्पणियाँ, समीक्षाएँ, शुभकामनाएँ छोड़ना न भूलें! सभी सामग्रियों की जांच एंटी-वायरस प्रोग्राम द्वारा की गई है।

ग्रेड 9 के लिए इंटीग्रल ऑनलाइन स्टोर में शिक्षण सहायक सामग्री और सिमुलेटर
ग्रेड 9 के लिए इंटरैक्टिव पाठ्यपुस्तक "ज्यामिति में नियम और अभ्यास"
ग्रेड 7-9 के लिए इलेक्ट्रॉनिक पाठ्यपुस्तक "समझने योग्य ज्यामिति"।

असमानताओं की प्रणाली

दोस्तों, आपने रैखिक और द्विघात असमानताओं का अध्ययन किया है और इन विषयों पर समस्याओं को हल करना सीखा है। आइए अब गणित की एक नई अवधारणा - असमानताओं की प्रणाली - की ओर बढ़ते हैं। असमानताओं की प्रणाली समीकरणों की प्रणाली के समान है। क्या आपको समीकरणों की प्रणालियाँ याद हैं? आपने सातवीं कक्षा में समीकरणों की प्रणालियों का अध्ययन किया था, यह याद करने का प्रयास करें कि आपने उन्हें कैसे हल किया था।

आइए हम असमानताओं की प्रणाली की परिभाषा का परिचय दें।
यदि आपको x के सभी मान ज्ञात करने की आवश्यकता है, तो कुछ चर x के साथ कई असमानताएँ असमानताओं की एक प्रणाली बनाती हैं, जिसके लिए प्रत्येक असमानता एक सही संख्यात्मक अभिव्यक्ति बनाती है।

x का कोई भी मान जिसके लिए प्रत्येक असमानता सही संख्यात्मक अभिव्यक्ति लेती है, असमानता का समाधान है। इसे निजी समाधान भी कहा जा सकता है।
निजी समाधान क्या है? उदाहरण के लिए, उत्तर में हमें अभिव्यक्ति x>7 प्राप्त हुई। तब x=8, या x=123, या सात से बड़ी कोई अन्य संख्या एक विशेष समाधान है, और अभिव्यक्ति x>7 एक सामान्य समाधान है। सामान्य समाधान कई निजी समाधानों से बनता है।

हमने समीकरणों की प्रणाली को कैसे संयोजित किया? यह सही है, एक घुंघराले ब्रेस, और इसलिए वे असमानताओं के साथ भी ऐसा ही करते हैं। आइए असमानताओं की प्रणाली का एक उदाहरण देखें: $\begin(cases)x+7>5\\x-3
यदि असमानताओं की प्रणाली में समान अभिव्यक्तियाँ शामिल हैं, उदाहरण के लिए, $\begin(cases)x+7>5\\x+7
तो, इसका क्या मतलब है: असमानताओं की प्रणाली का समाधान ढूंढना?
असमानता का समाधान असमानता के आंशिक समाधानों का एक सेट है जो सिस्टम की दोनों असमानताओं को एक साथ संतुष्ट करता है।

हम असमानताओं की प्रणाली का सामान्य रूप इस प्रकार लिखते हैं $\begin(cases)f(x)>0\\g(x)>0\end(cases)$

आइए हम $Х_1$ को असमानता f(x)>0 के सामान्य समाधान के रूप में निरूपित करें।
$X_2$ असमानता g(x)>0 का सामान्य समाधान है।
$X_1$ और $X_2$ विशेष समाधानों का एक समूह हैं।
असमानताओं की प्रणाली का समाधान $X_1$ और $X_2$ दोनों से संबंधित संख्याएँ होंगी।
आइए सेट पर ऑपरेशन को याद करें। हम किसी समुच्चय के उन तत्वों को कैसे खोज सकते हैं जो एक साथ दोनों समुच्चयों से संबंधित हों? यह सही है, इसके लिए एक इंटरसेक्शन ऑपरेशन है। तो, हमारी असमानता का समाधान सेट $A= X_1∩ X_2$ होगा।

असमानताओं की प्रणालियों के समाधान के उदाहरण

आइए असमानताओं की प्रणालियों को हल करने के उदाहरण देखें।

असमानताओं की व्यवस्था को हल करें.
a) $\begin(cases)3x-1>2\\5x-10 b) $\begin(cases)2x-4≤6\\-x-4
समाधान।
ए) प्रत्येक असमानता को अलग से हल करें।
$3x-1>2; \; 3x>3; \; x>1$.
$5x-10
आइए अपने अंतरालों को एक निर्देशांक रेखा पर अंकित करें।

सिस्टम का समाधान हमारे अंतरालों का प्रतिच्छेदन खंड होगा। असमानता सख्त है, तो खंड खुला रहेगा.
उत्तर: (1;3).

बी) हम प्रत्येक असमानता को अलग से भी हल करेंगे।
$2x-4≤6; 2x≤ 10; एक्स ≤ $5.
$-x-4 -5$.


सिस्टम का समाधान हमारे अंतरालों का प्रतिच्छेदन खंड होगा। दूसरी असमानता सख्त है, तो खंड बाईं ओर खुला होगा।
उत्तर: (-5; 5]।

आइए संक्षेप में बताएं कि हमने क्या सीखा है।
मान लीजिए कि असमानताओं की प्रणाली को हल करना आवश्यक है: $\begin(cases)f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end(cases)$.
फिर, अंतराल ($x_1; x_2$) पहली असमानता का समाधान है।
अंतराल ($y_1; y_2$) दूसरी असमानता का समाधान है।
असमानताओं की प्रणाली का समाधान प्रत्येक असमानता के समाधानों का प्रतिच्छेदन है।

असमानताओं की प्रणाली में न केवल प्रथम-क्रम की असमानताएँ, बल्कि किसी अन्य प्रकार की असमानताएँ भी शामिल हो सकती हैं।

असमानताओं की प्रणाली को हल करने के लिए महत्वपूर्ण नियम।
यदि सिस्टम की असमानताओं में से किसी एक का कोई समाधान नहीं है, तो पूरे सिस्टम का कोई समाधान नहीं है।
यदि चर के किसी भी मान के लिए असमानताओं में से एक संतुष्ट है, तो प्रणाली का समाधान दूसरी असमानता का समाधान होगा।

उदाहरण।
असमानताओं की प्रणाली को हल करें:$\begin(cases)x^2-16>0\\x^2-8x+12≤0 \end(cases)$
समाधान।
आइए प्रत्येक असमानता को अलग से हल करें।
$x^2-16>0$.
$(x-4)(x+4)>0$।

आइए दूसरी असमानता को हल करें।
$x^2-8x+12≤0$.
$(x-6)(x-2)≤0$.

असमानता का समाधान अंतराल है।
आइए दोनों अंतरालों को एक ही रेखा पर खींचें और प्रतिच्छेदन खोजें।
अंतरालों का प्रतिच्छेदन खंड (4; 6] है।
उत्तर: (4;6].

असमानताओं की व्यवस्था को हल करें.
ए) $\begin(केस)3x+3>6\\2x^2+4x+4 बी) $\begin(केस)3x+3>6\\2x^2+4x+4>0\end(केस )$.

समाधान।
a) पहली असमानता का समाधान x>1 है।
आइए दूसरी असमानता के लिए विभेदक खोजें।
$D=16-4 * 2 * 4=-16$. $D आइए नियम को याद रखें: जब किसी एक असमानता का कोई समाधान नहीं होता है, तो पूरी प्रणाली के पास कोई समाधान नहीं होता है।
उत्तर: कोई समाधान नहीं है.

बी) पहली असमानता का समाधान x>1 है।
दूसरी असमानता सभी x के लिए शून्य से अधिक है। तब सिस्टम का समाधान पहली असमानता के समाधान से मेल खाता है।
उत्तर: x>1.

स्वतंत्र समाधान के लिए असमानताओं की प्रणालियों पर समस्याएं

असमानताओं की प्रणाली को हल करें:
a) $\begin(cases)4x-5>11\\2x-12 b) $\begin(cases)-3x+1>5\\3x-11 c) $\begin(cases)x^2-25 d) $\begin(cases)x^2-16x+55>0\\x^2-17x+60≥0 \end(cases)$
ई) $\begin(केस)x^2+36