Nodarbības plāns.

Attālums starp diviem punktiem uz taisnas līnijas.

Taisnstūra (Dekarta) koordinātu sistēma.

Attālums starp diviem punktiem uz taisnas līnijas.

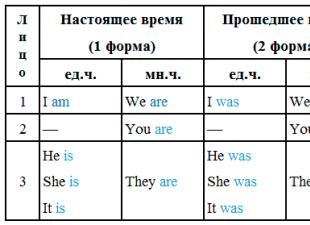
3. teorēma. Ja A(x) un B(y) ir jebkuri divi punkti, tad d - attālumu starp tiem aprēķina pēc formulas: d = lу - xl.

Pierādījums. Saskaņā ar 2. teorēmu mums ir AB = y - x. Bet attālums starp punktiem A un B ir vienāds ar nogriežņa AB garumu, tie. vektora AB garums. Tāpēc d \u003d lABl \u003d lu-xl.

Tā kā skaitļi y-x un x-y tiek ņemti modulo, mēs varam rakstīt d =lx-ul. Tātad, lai atrastu attālumu starp punktiem uz koordinātu līnijas, jums jāatrod to koordinātu starpības modulis.

4. piemērs. Doti punkti A(2) un B(-6), atrodiet attālumu starp tiem.

Lēmums. Formulā aizstājiet x=2 un y=-6. Iegūstam, AB=lу-хl=l-6-2l=l-8l=8.

5. piemērs Konstruējiet punktu, kas ir simetrisks punktam M(4) attiecībā pret sākuma punktu.

Lēmums. Jo no punkta M līdz punktam O 4 atsevišķi segmenti, atstāti malā pa labi, tad, lai izveidotu tam simetrisku punktu, mēs atlikam 4 atsevišķus segmentus no punkta O uz kreiso pusi, iegūstam punktu M "( -4).

6. piemērs Izveidojiet punktu C(x), kas ir simetrisks punktam A(-4) attiecībā pret punktu B(2).

Lēmums. Atzīmējiet punktus A(-4) un B(2) uz skaitļu līnijas. Attālumu starp punktiem atrodam pēc 3. teorēmas, iegūstam 6. Tad arī attālumam starp punktiem B un C jābūt vienādam ar 6. No punkta B pa labi noliekam 6 vienību segmentus, iegūstam punktu C (8) .

Vingrinājumi. 1) Atrodiet attālumu starp punktiem A un B: a) A(3) un B(11), b) A(5) un B(2), c) A(-1) un B(3), d) A (-5) un B (-3), e) A (-1) un B (3), (Atbilde: a) 8, b) 3, c) 4, d) 2, e) 2).

2) Konstruē punktu C(x), kas ir simetrisks punktam A(-5) attiecībā pret punktu B(-1). (Atbilde: C(3)).

Taisnstūra (Dekarta) koordinātu sistēma.

Veidojas divas savstarpēji perpendikulāras asis Ox un Oy, kam ir kopīga izcelsme O un viena mēroga mērvienība taisnstūrveida(vai Dekarta) koordinātu sistēma plaknē.

Vērša asi sauc x-ass, un y ass y ass. Tiek saukts asu krustošanās punkts O izcelsmi. Plakni, kurā atrodas Ox un Oy asis, sauc par koordinātu plakni un apzīmē ar Oxy.

Ļaujiet M ir plaknes patvaļīgs punkts. Atmetīsim no tā perpendikulus MA un MB attiecīgi uz asīm Ox un Oy. Tiek izsaukti abu perpendikulu krustošanās punkti A un B ar asīm prognozes punktu M uz koordinātu ass.

Punkti A un B atbilst noteiktiem skaitļiem x un y - to koordinātes uz asīm Ox un Oy. Tiek izsaukts cipars x abscisa punkti M, numurs y - viņa ordinātas.

To, ka punktam M ir koordinātas x un y, simboliski apzīmē šādi: M (x, y). Šajā gadījumā pirmais iekavās norāda abscisu, bet otrais - ordinātu. Sākumpunktam ir koordinātas (0,0).

Tādējādi ar izvēlēto koordinātu sistēmu katrs plaknes punkts M atbilst skaitļu pārim (x, y) - tā taisnstūra koordinātas un, otrādi, katram skaitļu pārim (x, y) atbilst, un turklāt viens, punkts M uz Oxy plaknes tā, ka tā abscisa ir x un ordināta ir y.

Tātad taisnstūrveida koordinātu sistēma plaknē nosaka vienu pret vienu atbilstību starp visu plaknes punktu kopu un skaitļu pāru kopu, kas ļauj pielietot algebriskās metodes, risinot ģeometriskās problēmas.

Koordinātu asis sadala plakni četrās daļās, tās sauc ceturtdaļas, kvadranti vai koordinātu leņķi un numurēti ar romiešu cipariem I, II, III, IV, kā parādīts attēlā (hipersaite).

Attēlā redzamas arī punktu koordinātu zīmes atkarībā no to atrašanās vietas. (piemēram, pirmajā ceturksnī abas koordinātas ir pozitīvas).

7. piemērs Būvpunkti: A(3;5), B(-3;2), C(2;-4), D (-5;-1).

Lēmums. Konstruēsim punktu A(3;5). Pirmkārt, mēs ieviešam taisnstūra koordinātu sistēmu. Pēc tam pa abscisu asi mēs noliekam 3 skalas vienības pa labi un pa ordinātu asi 5 mēroga vienības uz augšu, un caur galīgajiem dalīšanas punktiem novelkam taisnas līnijas, kas ir paralēlas koordinātu asīm. Šo taisnu krustpunkts ir nepieciešamais punkts A(3;5). Pārējie punkti tiek konstruēti tādā pašā veidā (skatiet hipersaites attēlu).

Vingrinājumi.

Nezīmējot punktu A(2;-4), noskaidro, kurai ceturtdaļai tas pieder.

Kurās ceturtdaļās var atrasties punkts, ja tā ordināta ir pozitīva?

Uz Oy ass tiek ņemts punkts ar koordinātu -5. Kādas ir tās koordinātas lidmašīnā? (atbilde: tā kā punkts atrodas uz Oy ass, tad tā abscisa ir 0, ordināta ir dota ar nosacījumu, tātad punkta koordinātas ir (0; -5)).

Punktus piešķir: a) A(2;3), b) B(-3;2), c) C(-1;-1), d) D(x;y). Atrodiet to punktu koordinātas, kas ir simetriski tiem ap x asi. Uzzīmējiet visus šos punktus. (atbilde: a) (2; -3), b) (-3; -2), c) (-1; 1), d) (x; -y)).

Punktus piešķir: a) A(-1;2), b) B(3;-1), c) C(-2;-2), d) D(x;y). Atrodiet to punktu koordinātas, kas ir simetriski tiem ap y asi. Uzzīmējiet visus šos punktus. (atbilde: a) (1; 2), b) (-3; -1), c) (2; -2), d) (-x; y)).

Punktus piešķir: a) A(3;3), b) B(2;-4), c) C(-2;1), d) D(x;y). Atrodiet to punktu koordinātas, kas tiem ir simetriskas par izcelsmi. Uzzīmējiet visus šos punktus. (atbilde: a) (-3; -3), b) (-2; 4), c) (2; -1), d) (-x;-y)).

Dots punkts M(3;-1). Atrodiet punktu koordinātas, kas ir simetriski tai ap Vērša asi, Oy asi un sākumpunktu. Uzzīmējiet visus punktus. (atbilde: (3;1), (-3;-1), (-3;1)).

Nosakiet, kurās ceturtdaļās var atrasties punkts M (x; y), ja: a) xy> 0, b) xy< 0, в) х-у=0, г) х+у=0. (ответ: а) в первой и третьей, б)во второй и четвертой, в) в первой и третьей, г) во второй и четвертой).

Nosakiet vienādmalu trijstūra virsotņu koordinātes, kuru mala ir vienāda ar 10 un atrodas pirmajā kvadrantā, ja viena no tā virsotnēm sakrīt ar sākumpunktu O un trijstūra pamatne atrodas uz Vērša ass. Izveidojiet zīmējumu. (atbilde: (0;0), (10;0), (5;5v3)).

Izmantojot koordinātu metodi, nosaka visu regulārā sešstūra ABCDEF virsotņu koordinātas. (atbilde: A (0;0), B (1;0), C (1,5;v3/2) , D (1;v3), E (0;v3 ), F (-0,5;v3 /2). Norāde: par koordinātu sākumpunktu ņemiet punktu A, virziet abscisu asi no A uz B, par skalas vienību ņemiet malas AB garumu. Ir ērti zīmēt lielas sešstūra diagonāles.)

Attālums no punkta līdz punktam ir segmenta garums, kas savieno šos punktus noteiktā mērogā. Tādējādi, runājot par attāluma mērīšanu, ir jāzina skala (garuma mērvienība), kurā tiks veikti mērījumi. Tāpēc problēmu atrast attālumu no punkta līdz punktam parasti aplūko vai nu uz koordinātu līnijas, vai taisnstūra Dekarta koordinātu sistēmā plaknē vai trīsdimensiju telpā. Citiem vārdiem sakot, visbiežāk attālums starp punktiem ir jāaprēķina pēc to koordinātām.

Šajā rakstā mēs, pirmkārt, atgādinām, kā tiek noteikts attālums no punkta līdz punktam uz koordinātu līnijas. Tālāk mēs iegūstam formulas attāluma aprēķināšanai starp diviem plaknes vai telpas punktiem pēc dotajām koordinātām. Noslēgumā mēs detalizēti apsveram tipisku piemēru un problēmu risinājumus.

Lapas navigācija.

Attālums starp diviem punktiem uz koordinātu līnijas.

Vispirms definēsim apzīmējumu. Attālums no punkta A līdz punktam B tiks apzīmēts kā .

No tā mēs varam secināt, ka attālums no punkta A ar koordinātu līdz punktam B ar koordinātu ir vienāds ar koordinātu starpības moduli, t.i., jebkuram punktu izvietojumam uz koordinātu līnijas.

Attālums no punkta līdz punktam plaknē, formula.

Iegūsim formulu, kā aprēķināt attālumu starp punktiem un dots taisnstūra Dekarta koordinātu sistēmā plaknē.

Atkarībā no punktu A un B atrašanās vietas ir iespējamas šādas iespējas.

Ja punkti A un B sakrīt, tad attālums starp tiem ir nulle.

Ja punkti A un B atrodas uz taisnas līnijas, kas ir perpendikulāra x asij, tad punkti un sakrīt, un attālums ir vienāds ar attālumu. Iepriekšējā rindkopā mēs noskaidrojām, ka attālums starp diviem punktiem uz koordinātu līnijas ir vienāds ar to koordinātu starpības moduli, tāpēc . Līdz ar to,.

Līdzīgi, ja punkti A un B atrodas uz taisnes, kas ir perpendikulāra y asij, tad attālums no punkta A līdz punktam B tiek atrasts kā .

Šajā gadījumā trijstūrim ABC ir taisnstūrveida konstrukcija un un . Autors Pitagora teorēma mēs varam uzrakstīt vienlīdzību , no kurienes .

Apkoposim visus rezultātus: attālumu no punkta līdz punktam plaknē nosaka caur punktu koordinātām pēc formulas .

Iegūto formulu attāluma starp punktiem noteikšanai var izmantot, ja punkti A un B sakrīt vai atrodas uz taisnes, kas ir perpendikulāra vienai no koordinātu asīm. Patiešām, ja A un B ir vienādi, tad . Ja punkti A un B atrodas uz taisnas līnijas, kas ir perpendikulāra Vērša asij, tad . Ja A un B atrodas uz taisnes, kas ir perpendikulāra Oy asij, tad .

Attālums starp punktiem telpā, formula.

Ieviesīsim telpā taisnstūra koordinātu sistēmu Оxyz. Iegūstiet formulu attāluma noteikšanai no punkta līdz punktam .

Kopumā punkti A un B neatrodas plaknē, kas ir paralēla vienai no koordinātu plaknēm. Zīmēsim caur punktiem A un B plaknē, kas ir perpendikulāra koordinātu asīm Ox, Oy un Oz. Šo plakņu krustošanās punkti ar koordinātu asīm dos mums punktu A un B projekcijas uz šīm asīm. Apzīmējiet projekcijas .

Vēlamais attālums starp punktiem A un B ir attēlā redzamā taisnstūra paralēlskaldņa diagonāle. Pēc konstrukcijas šī paralēlskaldņa izmēri ir un . Vidusskolas ģeometrijas kursā tika pierādīts, ka taisnstūra paralēlskaldņa diagonāles kvadrāts ir vienāda ar summu tā trīs dimensiju kvadrāti, tāpēc . Pamatojoties uz šī raksta pirmās sadaļas informāciju, mēs varam uzrakstīt šādas vienādības, tāpēc

kur mēs nonākam formula attāluma noteikšanai starp punktiem telpā .

Šī formula ir spēkā arī tad, ja punkti A un B

• mačs;
• pieder pie vienas no koordinātu asīm vai taisnes, kas ir paralēla vienai no koordinātu asīm;
• pieder vienai no koordinātu plaknēm vai plaknei, kas ir paralēla vienai no koordinātu plaknēm.

Attāluma atrašana no punkta līdz punktam, piemēri un risinājumi.

Tātad, mēs esam saņēmuši formulas attāluma noteikšanai starp diviem koordinātu līnijas punktiem, plakni un trīsdimensiju telpu. Ir pienācis laiks apsvērt tipisku piemēru risinājumus.

Problēmu skaits, kurās pēdējais solis ir atrast attālumu starp diviem punktiem pēc to koordinātām, ir patiešām milzīgs. Pilns apskatsšādi piemēri ir ārpus šī raksta darbības jomas. Šeit mēs aprobežojamies ar piemēriem, kuros ir zināmas divu punktu koordinātas un ir jāaprēķina attālums starp tiem.

Matemātikā gan algebra, gan ģeometrija rada problēmas atrast attālumu līdz punktam vai līnijai no dotā objekta. Tas atrodas pilnībā Dažādi ceļi, kuras izvēle ir atkarīga no sākotnējiem datiem. Apsveriet, kā noteikt attālumu starp dotajiem objektiem dažādos apstākļos.

Sākotnējā matemātikas zinātnes apgūšanas posmā viņi māca izmantot elementārus rīkus (piemēram, lineālu, transportieri, kompasu, trīsstūri un citus). Atrast attālumu starp punktiem vai līnijām ar to palīdzību nemaz nav grūti. Pietiek pievienot iedalījumu skalu un pierakstīt atbildi. Ir tikai jāzina, ka attālums būs vienāds ar taisnes garumu, ko var novilkt starp punktiem, un paralēlu līniju gadījumā - perpendikulu starp tiem.

Ģeometrijas teorēmu un aksiomu izmantošana

Iemācieties izmērīt attālumu bez palīdzības īpašas ierīces vai Tam nepieciešamas daudzas teorēmas, aksiomas un to pierādījumi. Bieži uzdevumi, kā atrast distanci, nonāk veidojumā un tā pušu meklēšanā. Lai atrisinātu šādas problēmas, pietiek zināt Pitagora teorēmu, trīsstūru īpašības un to pārveidošanu.

Ja ir divi punkti un norādīts to novietojums uz koordinātu ass, tad kā atrast attālumu no viena līdz otram? Risinājums ietvers vairākas darbības:

1. Mēs savienojam punktus ar taisnu līniju, kuras garums būs attālums starp tiem.
2. Atrodiet atšķirību starp katras ass punktu (k; p) koordinātu vērtībām: |k 1 - k 2 |= d 1 un | p 1 - p 2 |= d 2 (ņemam vērtības ​modulo, jo attālums nevar būt negatīvs).
3. Pēc tam iegūtos skaitļus savelkam kvadrātā un atrodam to summu: d 1 2 + d 2 2
4. Pēdējais solis ir iegūt no iegūtā skaitļa. Tas būs attālums starp punktiem: d \u003d V (d 1 2 + d 2 2).

Rezultātā viss risinājums tiek veikts pēc vienas formulas, kur attālums ir vienāds ar kvadrātsakni no koordinātu starpības kvadrātu summas:

d \u003d V (| k 1 - k 2 | 2 + | p 1 - p 2 | 2)

Ja rodas jautājums, kā atrast attālumu no viena punkta līdz otram, tad atbildes meklējumi uz to daudz neatšķirsies no iepriekš minētā. Lēmums tiks pieņemts pēc šādas formulas:

d \u003d V ( | k 1 - k 2 | 2 + | p 1 - p 2 | 2 + | e 1 - e 2 | 2)

Perpendikuls, kas novilkts no jebkura punkta, kas atrodas uz vienas taisnes, uz paralēli būs attālums. Risinot uzdevumus plaknē, ir jāatrod jebkuras līnijas jebkura punkta koordinātas. Un tad aprēķiniet attālumu no tā līdz otrajai taisnei. Lai to izdarītu, mēs tos nogādājam vispārējs skats Ah+By+C=0. No paralēlo līniju īpašībām ir zināms, ka to koeficienti A un B būs vienādi. Šajā gadījumā jūs varat atrast pēc formulas:

d \u003d | C 1 - C 2 | / V (A 2 + B 2)

Tādējādi, atbildot uz jautājumu, kā atrast attālumu no dotā objekta, ir jāvadās pēc problēmas stāvokļa un tās risināšanai paredzētajiem instrumentiem. Tās var būt gan mērierīces, gan teorēmas un formulas.

§ 1 Noteikums attāluma noteikšanai starp koordinātu līnijas punktiem

Šajā nodarbībā mēs atvasināsim noteikumu attāluma noteikšanai starp koordinātu līnijas punktiem, kā arī iemācīsimies atrast segmenta garumu, izmantojot šo noteikumu.

Izpildīsim uzdevumu:

Salīdziniet izteiksmes

1. a = 9, b = 5;

2. a = 9, b = -5;

3. a = -9, b = 5;

4. a = -9, b = -5.

Aizstājiet vērtības izteiksmēs un atrodiet rezultātu:

9 un 5 starpības modulis ir modulis 4, modulis 4 ir 4. 5 un 9 starpības modulis ir modulis mīnus 4, modulis -4 ir 4.

Starpības modulis starp 9 un -5 ir vienāds ar moduli 14, modulis 14 ir vienāds ar 14. Atšķirības modulis mīnus 5 un 9 ir vienāds ar moduli -14, modulis ir -14=14.

Starpības modulis mīnus 9 un 5 ir vienāds ar moduli mīnus 14, modulis mīnus 14 ir 14. 5 un mīnus 9 starpības modulis ir modulis 14, modulis 14 ir 14

Starpības modulis mīnus 9 un mīnus 5 ir vienāds ar moduli mīnus 4, modulis -4 ir 4. Modulis no starpības mīnus 5 un mīnus 9 ir vienāds ar moduli 4, modulis 4 ir (l-9 - (-5)l \u003d l-4l \u003d 4; l -5 - (-9)l = l4l = 4)

Katrā gadījumā tika iegūti vienādi rezultāti, tāpēc varam secināt:

Starpības a un b moduļa un starpības b un a moduļa izteiksmju vērtības ir vienādas jebkurai a un b vērtībai.

Vēl viens uzdevums:

Atrodiet attālumu starp koordinātu līnijas punktiem

1.A(9) un B(5)

2.A(9) un B(-5)

Uz koordinātu līnijas atzīmējiet punktus A(9) un B(5).

Saskaitīsim vienības segmentu skaitu starp šiem punktiem. Tie ir 4, kas nozīmē, ka attālums starp punktiem A un B ir 4. Tāpat mēs atrodam attālumu starp diviem citiem punktiem. Mēs atzīmējam punktus A (9) un B (-5) uz koordinātu līnijas, nosaka attālumu starp šiem punktiem pa koordinātu līniju, attālums ir 14.

Salīdziniet rezultātus ar iepriekšējiem uzdevumiem.

Starpības modulis starp 9 un 5 ir 4, un attālums starp punktiem ar koordinātām 9 un 5 arī ir 4. Starpības modulis starp 9 un mīnus 5 ir 14, attālums starp punktiem ar koordinātām 9 un mīnus 5 ir 14.

Tas liek secināt:

Attālums starp koordinātu taisnes punktiem A(a) un B(b) ir vienāds ar šo punktu koordinātu starpības moduli l a - b l.

Turklāt attālumu var atrast arī kā starpības moduli starp b un a, jo vienību segmentu skaits nemainīsies no punkta, no kura mēs tos skaitīsim.

2. § Noteikums, kā noteikt segmenta garumu pēc divu punktu koordinātām

Atrodiet segmenta CD garumu, ja uz koordinātu taisnes С(16), D(8).

Mēs zinām, ka segmenta garums ir vienāds ar attālumu no viena segmenta gala līdz otram, t.i. no punkta C uz punktu D uz koordinātu līnijas.

Izmantosim noteikumu:

un atrast koordinātu c un d starpības moduli

Tātad segmenta CD garums ir 8.

Apsveriet citu gadījumu:

Atrodiet segmenta MN garumu, kura koordinātas ir dažādas zīmes M (20), N (-23).

Aizstājiet vērtības

mēs zinām, ka -(-23) = +23

tātad 20 un mīnus 23 starpības modulis ir vienāds ar 20 un 23 summas moduli

Atradīsim dotā segmenta koordinātu moduļu summu:

Koordinātu starpības moduļa vērtība un koordinātu moduļu summa šajā gadījumā izrādījās vienāda.

Mēs varam secināt:

Ja divu punktu koordinātām ir dažādas zīmes, tad attālums starp punktiem ir vienāds ar koordinātu moduļu summu.

Nodarbībā iepazināmies ar noteikumu attāluma atrašanai starp diviem koordinātu līnijas punktiem un uzzinājām, kā, izmantojot šo noteikumu, var atrast atzara garumu.

Izmantotās literatūras saraksts:

1. Matemātika. 6. klase: stundu plāni mācību grāmatai I.I. Zubareva, A.G. Mordkovičs // Sastādījis L.A. Topilin. – M.: Mnemosyne 2009.
2. Matemātika. 6. klase: mācību grāmata izglītības iestāžu audzēkņiem. I.I. Zubareva, A.G. Mordkovičs. - M.: Mnemosyne, 2013. gads.
3. Matemātika. 6. klase: mācību grāmata izglītības iestāžu audzēkņiem./N.Ya. Viļenkins, V.I. Žohovs, A.S. Česnokovs, S.I. Švarcburds. - M.: Mnemosyne, 2013. gads.
4. Matemātikas rokasgrāmata - http://lyudmilanik.com.ua
5. Rokasgrāmata vidusskolas skolēniem http://shkolo.ru

Attālums starp punktiem uz koordinātu līnijas - 6 klase.

Formula attāluma noteikšanai starp punktiem koordinātu taisnē

Algoritms punkta koordināšu atrašanai - segmenta vidusdaļa

Paldies kolēģiem internetā, kuru materiālu izmantoju šajā prezentācijā!

Lejupielādēt:

Priekšskatījums:

Lai izmantotu prezentāciju priekšskatījumu, izveidojiet Google kontu (kontu) un pierakstieties: https://accounts.google.com

Slaidu paraksti:

Attālums starp punktiem uz koordinātu līnijas x 0 1 A B AB \u003d ρ (A, B)

Attālums starp punktiem uz koordinātu līnijas Nodarbības mērķis: - Atrodiet veidu (formulu, noteikumu), kā noteikt attālumu starp punktiem uz koordinātu līnijas. - Iemācieties atrast attālumu starp punktiem koordinātu taisnē, izmantojot atrasto noteikumu.

1. Mutiskā skaitīšana 15 -22 +8 -31 +43 -27 -14

2. Mutiski atrisiniet uzdevumu, izmantojot koordinātu līniju: cik veseli skaitļi ir ievietoti starp skaitļiem: a) - 8,9 un 2 b) - 10,4 un - 3,7 c) - 1,2 un 4,6? a) 10 b) 8 c) 6

0 1 2 7 pozitīvi skaitļi -1 -5 negatīvi skaitļi Attālums no mājām līdz stadionam 6 Attālums no mājām līdz skolai 6 Koordinātu līnija

0 1 2 7 -1 -5 Attālums no stadiona līdz mājām 6 Attālums no skolas līdz mājām 6 Attāluma noteikšana starp punktiem uz koordinātu līnijas ρ (-5 ; 1)=6 ρ (7 ; 1)=6 Attālums starp punktiem tiks apzīmēts ar burtu ρ (rho)

0 1 2 7 -1 -5 Attālums no stadiona līdz mājām 6 Attālums no skolas līdz mājām 6 Attāluma noteikšana starp punktiem uz koordinātu līnijas ρ (-5 ; 1)=6 ρ (7 ; 1)=6 ρ (a; b) = ? | a-b |

Attālums starp punktiem a un b ir vienāds ar šo punktu koordinātu starpības moduli. ρ (a; b)= | a-b | Attālums starp punktiem uz koordinātu līnijas

Reāla skaitļa moduļa ģeometriskā nozīme a b a a=b b x x x Attālums starp diviem punktiem

0 1 2 7 -1 -5 Atrodiet attālumus starp punktiem uz koordinātu līnijas - 2 - 3 - 4 3 4 5 6 -6 ρ (-6 ; 2)= ρ (6 ; 3)= ρ (0 ; 7) = ρ (1 ; -4) = 8 3 7 5

0 1 2 7 -1 -5 Atrodiet attālumus starp punktiem uz koordinātu līnijas - 2 - 3 - 4 3 4 5 6 -6 ρ (2 ; -6)= ρ (3 ; 6)= ρ (7 ; 0) = ρ (-4 ; 1) = 8 3 7 5

Izvade: izteiksmes vērtības| a-b | un | b-a | ir vienādi jebkurām a un b = vērtībām

–16 –2 0 –3 +8 0 +4 +17 0 ρ(–3; 8) = 11; |(–3) – (+8)| = 11; |(+8) – (–3)| = 11. ρ(–16; –2) = 14; |(–16) – (–2)| = 14; |(–2) – (–16)| = 14. ρ(4; 17) = 13; |(+4) – (+17)| = 13; |(+17) – (+4)| = 13. Attālums starp koordinātu līnijas punktiem

Atrast ρ(x; y)ja: 1) x = -14, y = -23; ρ(x; y)=| x – y |=|–14–(– 23)|=|–14+23|=| 9 |=9 2) x = 5,9, y = -6,8; ρ(x; y)=|5, 9 –(– 6,8)|=|5,9+6,8|=| 12,7 |=12,7

Turpiniet teikumu 1. Koordinātu taisne ir taisne ar ... 2. Attālums starp diviem punktiem ir ... 3. Pretēji skaitļi ir skaitļi, ... 4. Skaitļa X moduli sauc par ... 5 - Salīdzināt izteiksmju vērtības a - b V b - a secināt … - Salīdzināt izteiksmju vērtības | a-b | v | b-a | c secinu...

Vintik un Shpuntik iet pa koordinātu staru. Skrūve atrodas punktā B(236), Shpuntik atrodas punktā W(193). Cik tālu Screw un Shpuntik atrodas viens no otra? ρ(B, W) = 43

Atrodiet attālumu starp punktiem A (0), B (1) A (2), B (5) A (0), B (- 3) A (- 10), B (1) AB \u003d 1 AB \u003d 3 AB \u003d 3 AB = 11

Atrodiet attālumu starp punktiem A (- 3,5), B (1,4) K (1,8), B (4,3) A (- 10), C (3)

Pārbaudiet AB = KV = AC =

C (- 5) C (- 3) Atrodiet punkta koordinātu - nogriežņa BA vidusdaļu

Uz koordinātu līnijas ir atzīmēti punkti A (–3,25) un B (2,65). Atrodiet punkta O koordinātu - nogriežņa AB viduspunktu. Risinājums: 1) ρ(А;В)= |–3,25 – 2,65| = |–5,9| \u003d 5,9 2) 5,9: 2 \u003d 2,95 3) -3,25 + 2,95 \u003d - 0,3 vai 2,65 - 2,95 \u003d - 0,3 Atbilde: O (-0, 3)

Uz koordinātu līnijas ir atzīmēti punkti С(–5.17) un D(2.33). Atrodiet punkta A koordinātu - segmenta CD viduspunktu. Risinājums: 1) ρ(С; D)= |– 5 , 17 – 2, 33 | = |– 7 , 5 | \u003d 7, 5 2) 7, 5: 2 \u003d 3, 7 5 3) - 5, 17 + 3, 7 5 \u003d - 1, 42 vai 2, 33 - 3, 7 5 \u003d - 1, 4 Atbilde: A (-1, 42)

Secinājums: Punkta koordinātes atrašanas algoritms - dotā segmenta vidus: 1. Atrodiet attālumu starp punktiem - dotā segmenta galiem = 2. Sadaliet rezultātu-1 ar 2 (puse vērtības) = ​​c 3. Pievienojiet rezultātu-2 koordinātei a vai atņemiet rezultātu-2 no koordinātas a + c vai - c 4. Rezultāts-3 ir punkta koordināte - dotā segmenta vidusdaļa.

Darbs ar mācību grāmatu: §19, 112. lpp., A. Nr. 573, 575 V. Nr. 578, 580 Mājasdarbs: §19, 112. lpp., A. Nr. 574, 576, B. Nr. 579, 581 sagatavot CD “Racionālo skaitļu saskaitīšana un atņemšana. Attālums starp punktiem uz koordinātu līnijas "

Šodien es iemācījos... Bija interesanti... Es sapratu, ka... Tagad es varu... Es iemācījos... Man izdevās... Es mēģināšu... Es biju pārsteigts... Es gribēju...